Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Readln(x);. 1) видим, что в последний строках выводятся на экран переменные a и b, поэтому сначала нужно определить

a: = 0; b: = 0;

while x > 0 do begin

c: = x mod 2;

if c = 0 then a: = a + 1

else b: = b + 1;

x: = x div 10;

End;

Writeln(a);

Writeln(b);

End.

Решение:

1) видим, что в последний строках выводятся на экран переменные a и b, поэтому сначала нужно определить, что они обозначают в программе

2) перед началом цикла обе переменные обнуляются

3) на каждом шаге цикла при выполнении некоторого условия переменная a увеличивается на 1, а если это условие не выполняется, то на 1 увеличивается b; таким образом, обе переменных – счётчики

4) теперь посмотрим на условие c = 0: в предыдущей строке в переменную c записывается остаток от деления числа x на 2, то есть, переменная c определяет четность числа или, что равносильно, чётность его последней цифры

5) если последняя цифра чётная, то увеличивается счётчик a, а если нечётная – увеличивается счётчик b

6) в конце каждого шага цикла операция x: =x div 10 отсекает последнюю цифру в десятичной записи числа

7) таким образом, делаем вывод: после завершения цикла в переменной a находится количество чётных цифр в десятичной записи числа, а в переменно b – количество нечётных цифр

8) если было выведено 3 и 2, то в числа 5 цифр, из них 3 чётных и 2 нечётных; таким образом, нам нужно найти минимальное пятизначное число, в котором 3 чётные и 2 нечётные цифры

9) минимальная чётная цифра – это 0, минимальная начётная – 1; 0 не может стоять на первом месте, поэтому число начинается с 1

10) для получения минимального числа после 1 должны идти нули и последняя цифра – снова 1

11) ответ: 10001

Ещё пример задания:

P-02. Ниже записан алгоритм. После выполнения алгоритма было напечатано 3 числа. Первые два напечатанных числа – это числа 9 и 81. Какое наибольшее число может быть напечатано третьим?

var x, y, z: integer;

r, a, b: integer;

Begin

Readln(x, у);

if у > x then begin

z: = x; x: = у; у: = z;

End;

a: = x; b: = y;

while b > 0 do begin

r: = a mod b;

a: = b;

b: = r;

End;

Writeln(a);

Writeln(x);

Write(у);

End.

Решение:

1) сложность этой задачи состоит в том, чтобы разобраться в алгоритме

2) сначала вводятся два числа и переставляются так, чтобы в переменной x было наибольшее число, а в переменной y – наименьшее из двух:

if у > x then begin

z: = x; x: = у; у: = z;

End;

3) затем исходные значения копируются в переменные a и b и с ними выполняется следующий алгоритм

while b > 0 do begin

r: = a mod b;

a: = b;

b: = r;

End;

его суть сводится к тому, что меньшее из двух чисел, a и b, каждый раз заменяется на остаток от деления большего на меньшее до тех пор, пока этот остаток не станет равен нулю;

4) делаем вывод, что это классический Алгоритм Евклида, который служит для вычисления наибольшего общего делителя (НОД) двух чисел; это делитель в результате оказывается в переменной a

5) смотрим, что выводится на экран: сначала значение переменной a (наибольший общий делитель исходных чисел, НОД(x, y)), затем значение x (большее из исходных чисел) и значение y (меньшее из исходных чисел)

6) по условию первое число – 9, второе – 81, поэтому третье число должно быть меньше, чем 81, и НОД(81, y) = 9

7) наибольшее число, которое меньше 81 и делится на 9, равно 72 (обратите внимание, что исходные числа не могут быть равны, потому что в этом случае их НОД был бы равен 81)

8) ответ: 72

Ещё пример задания:

P-01. Ниже записана программа. Получив на вход число 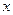, эта программа печатает два числа, 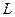и 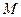. Укажите наибольшее из таких чисел 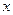, при вводе которых алгоритм печатает сначала 3, а потом 7.

var x, L, M: integer;

Begin