Графоаналітичний метод знаходження екстремуму лінійної функції двох змінних при заданій системі лінійних обмежень.

💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Задача лінійного програмування може бути геометрично інтерпретована у такий спосіб: накладені обмеження (4*) на змінні, які необхідно знайти хj геометрично зображуються деякою областю W, яка утворює випуклий багатогранник в п - мірному просторі. Ця область називається областю припустимих планів, оскільки будь-яка точка в її межах відповідає вимогам (4*). З усіх припустимих планів нас цікавить оптимальний план, при якому цільова функція (3*) досягає оптимуму (максимуму чи мінімуму), тобто серед усіх точок багатокутної області W треба знайти ту, яка звертає у максимум цільову функцію (3*). При цьому оптимальне рішення, якщо воно існує, обов’язково досягається в будь-якій вершині багатогранника. Щоб знайти розв’язок задачі лінійного програмування, досить розглянути лише ті плани, які відповідають вершинам багатогранника. Таки плани називаються опорними.

Розглянута геометрична інтерпретація задачі лінійного програмування можлива лише при наявності двох незалежних змінних. При трьох змінних наочне представлення значно ускладнюється, тому що в цьому випадку має місце деякий випуклий багатогранник у тривимірному просторі, що відповідає обсягу припустимих планів.

Цільовій функції Z відповідає сімейство паралельних прямих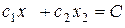

. Пам'ятаючи те, що напрям найшвидшого зростання функції Z вказує вектор

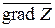, знайдемо координати цього вектора

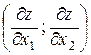Означення. Пряма, яка може рухатися у напрямі найшвидшого зростання функції Z називається опорною прямою.

Якщо будемо рухати опорну пряму в напрямі вектора-градієнта, то перша спільна точка даної прямої і многокутника W буде точкою мінімуму цільової функції, а остання спільна точка – точкою максимуму.

Зауваження. Метод знаходження опорної прямої у випадку рішення задачі лінійного програмування може бути спрощеним. Так як цільова функція лінійна, тобто вона описується рівнянням прямої, то коефіцієнти при змінних в цьому рівнянні дорівнюють координатам вектора-градієнта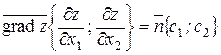

Для розв'язку задач графоаналітичним методом по знаходженню екстремуму лінійної функції двох змінних з заданою системою лінійних обмежень необхідно:

- побудувати багатокутник допустимих розв’язків нерівностей системи;

- побудувати вектор-градієнт від початку координат і опорну пряму;

- рухати опорну пряму в напрямку градієнта, якщо необхідно знайти точку максимуму цільової функції; якщо треба знайти точку мінімуму, опорну пряму необхідно рухати протилежно напрямку градієнта;

- обчислити координати знайдених точок та значення цільової функції в цих точках.

Зауваження. При розв’язуванні задачі лінійного програмування графічним методом можуть бути такі варіанти розв’язків:

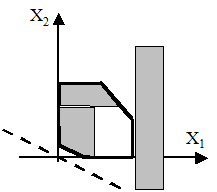
1. Задача не має розв’язку, оскільки система умов не сумісна, тобто не існує загальної області припустимих розв’язків – ОПР.

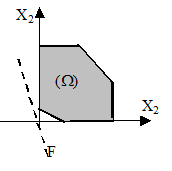2. Задача має один єдиний розв’язок, система умов сумісна і цільова функція досягає свого екстремального значення в одній з вершин

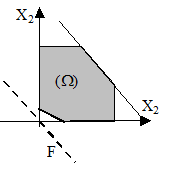
3. Задача має безліч розв’язків, тобто система умов сумісна, а цільова функція при прямуванні до екстремуму накладається на одну зі сторін багатокутника.

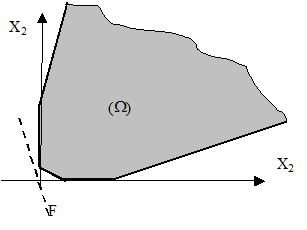
4. Задача не має розв’язку, оскільки ОПР не обмежена. Однак якщо ОПР не обмежена зверху, то цільова функція має тільки мінімум, якщо ОПР не обмежена знизу – цільова функція має тільки максимум.

Зауваження. При кількості змінних більш трьох задача втрачає геометричну наочність. Однак ідея одержання рішення зберігає зміст і для випадку багатомірного простору. Більш того, у багатьох випадках можна всі невідомі виразити через дві незалежні величини, вибрати ці величини як координатні вісі, представити обмеження і цільову функцію через них і вирішити задачу графоаналітичним методом.