💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Загальна постановка задачі лінійного програмування.

Розв'язання систем лінійних нерівностей.

Означення. Нерівність називається лінійною, якщо вона містить змінні тільки у першому ступені, причому добуток змінних відсутній.

Загальний вигляд лінійної нерівності з двома змінними наступний 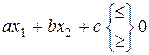. Ці нерівності називаються нестрогими. Нестрога нерівність еквівалентна рівнянню 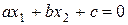і строгій нерівності .

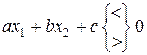Множиною рішень рівняння 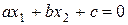є пряма, яка розбиває площину Х0У на дві півплощини. Множиною рішень нерівності 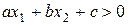є одна з цих півплощин. Щоб визначити, яка з них, потрібно вибрати контрольну точку (це може бути початок координат). Якщо координати контрольної точки являються рішенням нерівності, то координати всіх точок півплощини, на якій вибрана контрольна точка, теж є рішенням нерівності.

Означення. Множиною рішень лінійної нерівності 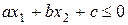є одна з півплощин, на яку пряма ділить площину Х0У, включаючи і цю пряму.

Приклад. Знайти множину розв’язків нерівності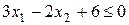

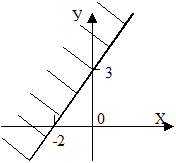Рішення:

Побудуємо пряму 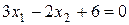за точками перетину цієї прямої з осями координат: А(-2; 0) – точка перетину з віссю 0Х1. В(0; 3) – точка перетину х віссю 0Х2.

За контрольну точку візьмемо точку 0(0; 0) – початок координат. Після підстановки координат х1 = 0 і х2 = 0 в нерівність одержимо 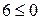- нерівність не виконується. Отже розв’язком є верхня напівплощина разом з прямою (заштрихована частина).

Означення. Множиною розв’язків системи лінійних рівнянь нерівностей із двома невідомими 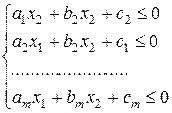є випуклий многокутник (крім випадку, коли система несумісна).

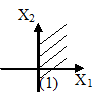Приклад. Знайти множину розв’язків системи: .

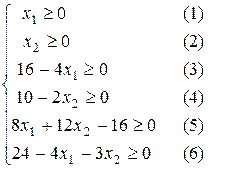Розв¢ язок.

1) Побудуємо множину розв'язків першої нерівності (1).

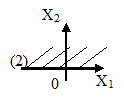
2) Побудуємо множину розв'язків нерівності (2).

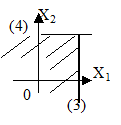
3) Побудуємо множину розв'язків нерівностей (3) і (4).

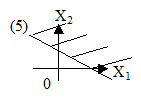
4) Побудуємо множину розв'язків нерівності (5).

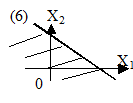
5) Побудуємо множину розв'язків нерівності (6).

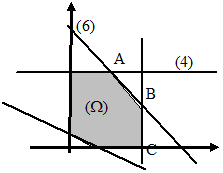Таким чином, розв'язком системи лінійних нерівностей є випуклий многокутник. Координати вершин цього многокутника можна знайти, розв’язавши систему лінійних рівнянь прямих, на перетині яких знаходяться вершини.

Наприклад, щоб знати координати точки А, розв'яжемо систему двох рівнянь (4) і (6) 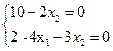Þ .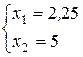

Звідси, вершина А має координати А(2, 25; 5).

Аналогічно можна визначити координати точки В(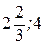), як точки перетинання прямих (3) і (2), точки С(4; 0), як точки перетинання прямих (3) і (6) і т.д.