Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Лабораторна робота № 1. Графоаналітичний метод рішення задач лінійного програмування.

МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

ОДЕСЬКИЙ ДЕРЖАВНИЙ АГРАРНИЙ УНІВЕРСИТЕТ

Кафедра землевпорядного проектування

Методичні вказівки

для розробки лабораторно – практичних робіт по курсу

“Математичні методи і моделі”

для студентів спеціальності 7.070900

“Землевпорядкування та кадастр”

Одеса 2004

Методичні вказівки для розробки лабораторно – практичних робіт по курсу “Математичні методи та моделі” склали професор Вікуліна Лідія Федорівна і викладач Друбецька Ірина Ігорівна - кафедра землевпорядного проектування Одеського державного аграрного університету.

Рецензія на методичні вказівки завідувача кафедри економічної кібернетики ОДАУ професора Сухорукова В. Ф. позитивна.

Розглянуто і затверджено на методичній раді факультету землевпорядкування 30 березня 2004 року, протокол № 7

Зміст

Вступ 4

Лабораторна робота № 1. Графоаналітичний метод рішення задач

лінійного програмування 7

1.1. Загальна постановка задачі лінійного програмування 7

1.2. Графоаналітичний метод знаходження екстремуму

лінійної функції двох змінних при заданій системі

лінійних обмежень 10

Лабораторна робота № 2. Обчислювальні методи

лінійного програмування 13

2.1. Загальна ідея симплекс – методу. 13

2.2. Алгоритм симплекс – методу. 15

Лабораторна робота № 3. Рішення задач лінійного

програмування на ПЕОМ симплекс – методом за

допомогою стандартної програми “Поиск решения” 24

3.1. Процедура пошуку рішення. 26

Варіанти завдань. 28

Список використаної літератури. 30

Вступ

Лінійне програмування застосовується для рішення задач, у яких необхідно оптимальним чином розподілити будь-які засоби з урахуванням накладених обмежень. Метод лінійного програмування дозволяє вирішувати ряд тактичних, оперативних і інших задач при наявності багатьох взаємозалежних факторів.

Для цього одну з, що аналізуються (наприклад, врожайність озимої пшениці), а також умови задачі виражають у вигляді функцій, що залежать від ряду змінних.

Потім знаходять оптимальне (максимальне чи мінімальне) значення цього критерію і відповідні йому значення змінних.

Змінними величинами можуть бути, наприклад, площа полів сівозміни, число зайнятих працівників, валовий збір врожаю та інші важливі показники.

В результаті рішення ми одержимо також значення змінних величин, дотримуючи яких забезпечимо оптимальний розподіл засобів.

Означення. Лінійне програмування - математичний метод знаходження максимуму чи мінімуму лінійної функції при наявності обмежень у вигляді лінійних рівнянь чи нерівностей.

Означення. Функція, яка максимізується (мінімізується) являє собою прийнятий критерій ефективності рішення задачі, що відповідає поставленій меті. Вона зветься цільовою функцією.

Обмеження характеризують наявні можливості рішення задачі.

Сутність рішення задач лінійного програмування полягає в тому, щоб знайти умови, що звертають цільову функцію в максимум чи мінімум.

Означення. Рішення, що найкраще відповідає цільовій настанові і задовольняє всім умовам задачі, називається оптимальним планом.

У загальному вигляді постановка задачі лінійного програмування виглядає таким чином.

Умови задачі задаються у вигляді системи лінійних рівнянь чи нерівностей, що представляють обмеження, які накладаються на використання наявних ресурсів:

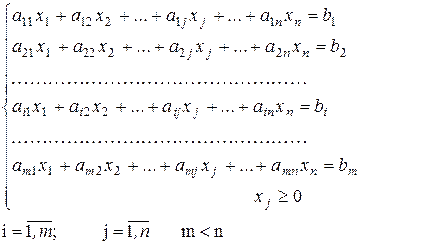(1*)

Цільова функція задається у вигляді лінійної форми:

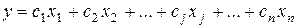(2*)

де х₁, х₂,..., х_n - величини, які необхідно знайти, вони не можуть бути від’ємними;

a_ij и b_i – відомі постійні величини, що характеризують умови задачі.

с_j - постійні коефіцієнти.

У короткій формі задача лінійного програмування має вигляд:

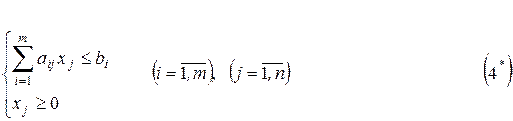
Зауваження. Якщо обмеження задаються у вигляді нерівностей, то вводячи в кожне лінійне обмеження додаткові невід'ємні невідомі можна привести систему лінійних обмежень до стандартного (канонічного) вигляду (1*). Зручно позначати ці додаткові змінні символами S₁, S₂, …, S_m (індекс m вказує на номер обмеження).

Існує кілька методів рішення задач лінійного програмування, у тому числі і симплекс-метод, який ми будемо використовувати. При великому числі змінних для рішення таких задач необхідно застосовувати ЕОМ. Найбільш загальні алгоритми рішення задач лінійного програмування наведені до стандартних програм і включені в математичне забезпечення ЕОМ (пошук рішення).

Якщо число змінних системи обмежень і цільової функції в математичній моделі задачі лінійного програмування дорівнює 2 чи 3, таку задачу можна вирішити графоаналітичним методом рішення задач лінійного програмування.

Лабораторна робота № 1. Графоаналітичний метод рішення задач лінійного програмування.