
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Биномиальное распределение дискретной случайной величины
|
|
Пусть проводится n независимых испытаний, в каждом из которых событие А наступает с вероятностью р (0 < p < 1), и не наступает с вероятностью q, q = 1 – p. Обозначим Pn (m) – вероятность того, что в n испытаниях событие А наступит ровно m раз, тогда случайная величина Х такая, что Р (Х = m) = Pn (m)определяет биномиальное распределение или распределение Бернулли. Вероятности Pn (m) вычисляются по формуле:
| Pn(m) = Cnmpm qn – m, | (1.16) |
где коэффициенты Cnm называются числом сочетаний из n элементов по m и вычисляют по формуле:
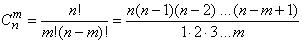 . .
| (1.17) |
Из формулы (1.17) видно, что Cnm = Cnn – m (m = 1, 2,,,,, n – 1).
По определению полагают также Cn 0 = Cnn = 1.
Рассмотрим смысл коэффициентов Cnm. Пусть заданы n разных элементов. Всевозможные группировки из данных n элементов по m элементов в каждой, отличающиеся друг от друга хотя бы одним элементом, при этом порядок расположения элементов в группировке безразличен, называются сочетаниями из n элементов по m. Например, n = 4, имеем 4 элемента: а, b, c, d. Выпишем сочетания из четырех элементов по два: ab, ac, ad, bc, bd, cd. Из определения следует, что сочетания ab и ba не различимы. Число таких сочетаний и находится по формуле (1.17), 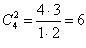 .
.
Примеры вычисления: 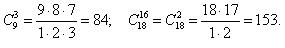
Вероятность того, что в n испытаниях событие А наступит менее m раз, равна сумме вероятностей:
Pn (0) + Pn (1) +... + Pn (m – 1);
более m раз – сумме вероятностей:
Pn (m + 1) +... + Pn (n).
Часто расчеты упрощаются, если применять свойство вероятностей Pn (m)
Pn (0) + Pn (1) +... + Pn (n) = 1.
Пример 1.10. В урне 10 шаров, из них 3 белых. Вынимают наугад 3 шара. Найти распределения вероятностей случайной величины Х – числа вынутых белых шаров при повторной выборке. При повторной выборке после каждого извлечения шара отмечают его цвет и возвращают шар в урну, снова перемешивая шары.
Решение: P (X = 0) = Р (три раза вынимали черный шар) = 0, 7 · 0, 7 · 0, 7, где 0, 7 – вероятность вынуть черный шар из урны. Так как после каждого извлечения шар возвращают в урну и шары перемешивают, то система шаров возвращается в исходное состояние и вероятность вынуть черный шар одинакова при любом извлечении.
P (X = 1) = Р (вынимали один белый шар и два черных) = Р (вынули белый шар первым или вынули белый шар вторым, или вынули белый шар третьим) =
= 0, 3 · 0, 7 · 0, 7+0, 7 · 0, 3 · 0, 7 + 0, 7 · 0, 7 · 0, 3 = 3 · 0, 3 · 0, 72 = 0, 441.
P (X = 2) = Р (вынимали один черный шар и два белых) = Р (вынули черный шар первым или вынули черный шар вторым, или вынули черный шар третьим) =
= 0, 7 · 0, 3 · 0, 3 + 0, 3 · 0, 7 · 0, 3 + 0, 3 · 0, 3 · 0, 7 = 3 · 0, 32 · 0, 7 = 0, 189.
P (X = 3) = Р (три раза вынимали белый шар) = 0, 3 · 0, 3 · 0, 3.
Распределение вероятностей случайной величины Х представлено в таблице 1.2.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Таблица 1.2
| X | P |
| 0, 73 = 0, 343 | |
| 3 · 0, 3 · 0, 72 = 0, 441 | |
| 3 · 0, 32 · 0, 7 = 0, 189 | |
| 0, 33 = 0, 027 | |
| ∑ | 1, 000 |
1.1.6 Числовые характеристики дискретных случайных величин
Случайные величины могут описываться числовыми характеристиками, среди которых различают характеристики положения (математическое ожидание, мода, медиана) и характеристики рассеяния (дисперсия, среднеквадратическое отклонение).
Математическое ожидание M (X) представляет собой среднее ожидаемое значение случайной величины. Если пространство элементарных исходов состоит из конечного числа взаимно исключающих друг друга возможных исходов ω 1, ω 2,..., ω N с вероятностями Р (ω i) = pi (i = 1, 2,..., N; 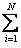 pi = 1), то математическое ожидание случайной величины Х = Х (ω), X (ω i) = xi, вычисляют по формуле:
pi = 1), то математическое ожидание случайной величины Х = Х (ω), X (ω i) = xi, вычисляют по формуле:
M (X) = 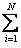 xi pi. xi pi.
| (1.18) |
Свойства математического ожидания:
1) M (C) = C, где С = const,
2) M (CX) = CM (X),
3) M (X + Y) = M (X) + M (Y) для любых случайных величин Х и Y,
4) M (XY) = M (X) · M (Y), если Х и Y независимы.
Таким образом, если случайная величина Х представлена в виде линейной комбинации величин X 1, X 2,..., XL, то ее математическое ожидание вычисляют по свойству линейности:
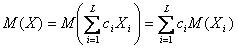 . .
| (1.19) |
Если известна таблица распределения дискретной случайной величины, то математическое ожидание любой ее функции может быть вычислено по формуле:
M (f (X)) = 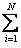 f (xi) · pi. f (xi) · pi.
| (1.20) |
Для характеристики степени разбросанности значений случайной величины около ее математического ожидания M (X) = а вводятся понятия дисперсии D (X) и среднего квадратического отклонения σ (X) по формулам:
D (X) = M (X – a)2; 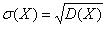
| (1.21) |
Свойства дисперсии и среднего квадратического отклонения:
1) D (C) = 0; σ (C) = 0, где С = const,
2) D (CX) = C 2 D (X); σ (CX) = | C |σ (X),
3) D (X + Y) = D (X) + D (Y), если Х и Y независимы.
Дисперсия для дискретной случайной величины Х может быть найдена по формуле:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
D (X) = M (X 2) – a 2 = 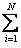 xi 2 pi – a 2. xi 2 pi – a 2.
| (1.22) |
Математическое ожидание и дисперсия дискретной случайной величины Х, имеющей биномиальное распределение, могут быть найдены по формулам:
| M (X) = np; D (X) = npq, | (1.23) |
где р – вероятность того, что событие А произойдет, q – вероятность того, что событие А не произойдет в каждом из независимых испытаний.
Содержание типового расчета
Типовой расчет состоит из двух задач. В каждой из них задана дискретная случайная величина. Требуется
1. Найти распределение этой случайной величины.
2. Провести контроль расчетов, сложив полученные вероятности. Их сумма должна быть равна единице.
3. Вычислить математическое ожидание М (Х), дисперсию D (X) и среднее квадратическое отклонение σ (Х) случайной величины Х.
4. Вычислить вероятность Р события, сформулированного в условии задачи.
5. Найти функцию распределения F (x) и построить ее график.
|
|
