Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Дискретные случайные величины

Если результатом эксперимента является число, значение которого нельзя предсказать точно до проведения самого эксперимента, то это число называют случайной величиной. Случайную величину называют дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или счетным.
Строгое определение дискретной случайной величины, принимающей конечное число различных значений следующее: это числовая функция Х (ω), определенная на пространстве элементарных исходов Ω, принимающая конечное число различных значений x ₁, x ₂,..., x_N. Ее распределение задается таблицей вида:

где x_i упорядочены по возрастанию x ₁ < x ₂ < x ₃ <... < x_N и p_i = P (X = x_i). Так как события X = x_i образуют полную группу, то 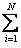p_i = 1, что часто служит контролем вычисления p_i.
Функцией распределения случайной величины Х является функция F (x), равная вероятности события (Х < x), т.е. вероятности того, что случайная величина Х примет значение, меньшее значения аргумента х, т.е.

Функция распределения обладает следующими свойствами:
1. 0 ≤ F ≤ 1 для всех х;
2. F (–∞) = 0, F (+∞) = 1;
3. F (x) – неубывающая функция на всей оси;
Вероятность попадания случайной величины Х в произвольный интервал [ x ₁, x ₂) определяется формулой:

Зная закон распределения дискретной случайной величины Х, можно вычислить функцию распределения, представляющую собой, в силу определения (1.13) функцию накопленных вероятностей:

,

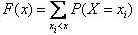(1.15)

где суммирование распространяется на все значения индекса i, для которых x_i < x.
Из этой формулы, в частности, следует, что
F (x_k + 0) – F (x_k) = P (X = x_k), x_k є { x ₁, x ₂,... },
т.е. функция распределения дискретной случайной величины Х испытывает скачки в точках х, для которых существует положительная вероятность события (X = x).

Пример 1.7. Три стрелка стреляют по мишени независимо друг от друга по одному разу. Вероятности попадания равны: для первого стрелка Р (A ₁) = 0, 7, для второго стрелка Р (A ₂) = 0, 8, для третьего стрелка Р (A ₃) = 0, 9. Найти распределения вероятностей случайной величины Х – числа попаданий в мишень.
Решение:
P (X = 0) = Р (не попали все три стрелка) = 0, 3 · 0, 2 · 0, 1 = 0, 006.
P (X = 1) = Р (попал только один стрелок) = Р (попал только первый стрелок или попал только второй стрелок, или попал только третий стрелок) = 0, 7 · 0, 2 · 0, 1 + 0, 3 · 0, 8 · 0, 1 + 0, 3 · 0, 2 · 0, 9 = 0, 092.
P (X = 2) = Р (не попал только один стрелок) = Р (не попал только первый стрелок или не попал только второй стрелок, или не попал только третий стрелок) = 0, 3 · 0, 8 · 0, 9 + 0, 7 · 0, 2 · 0, 9 + 0, 7 · 0, 8 · 0, 1 = 0, 398.
P (X = 3) = Р (попали все три стрелка) = 0, 7 · 0, 8 · 0, 9 = 0, 504.
Распределение вероятностей случайной величины Х представлено в таблице 1.1. Для контроля подсчитана сумма полученных вероятностей. Сумма равна единице.

Таблица 1.1

Пример 1.8. При условии задачи 1.7. найти вероятность того, что в мишень попали хотя бы два стрелка.
Решение: Требуется найти вероятность события X ≥ 2.
P (X ≥ 2) = P (X = 2) + P (X = 3) = 0, 398+0, 504 = 0, 902.

Пример 1.9. Дискретная случайная величина Х задана законом распределения:

Найти функцию распределения F (x) и построить ее график.
Решение: Найдем функцию распределения F (x).
1. Если x ≤ 1, то F (x) = 0. Действительно, значений меньших числа 1, величина Х не принимает. Следовательно, при x ≤ 1 функция F (x) = P (X < x) = 0.
2. Если 1 < x ≤ 3, то F (x)= 0, 2. Действительно, Х может принять значение 1 с вероятностью 0, 25.
3. Если 3 < x ≤ 6, то F (x) = 0, 55. Действительно, Х может принять значение 1 с вероятностью 0, 25 и значение 3 с вероятностью 0, 3. Следовательно, одно из этих значений Х может принять (по теореме сложения вероятностей несовместных событий) с вероятностью 0, 25 + 0, 3 = 0, 55.
4. Если x > 6, то F (x) = 1. Действительно, событие x > 6 достоверное и вероятность его равна 1.
Искомая функция распределения имеет вид: .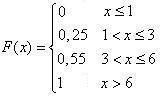
График этой функции приведен на рис. 1.1.

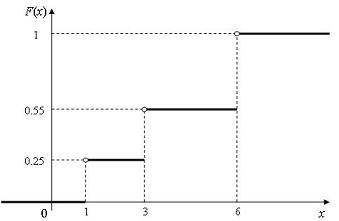
Рисунок 1.1