
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сериальные формулы
|
|
Вопрос о спектрах представляется одним из центральных в современной физике: сюда относятся, например, такие обширные отделы современной физики, как учение о строении атома и молекул, учение об изотопах и др.
Линейчатые спектры состоят из ряда тонких прямых линий, которые могут быть расположены как в видимой, так и в инфракрасной и в ультрафиолетовой частях спектра. В видимой части они представляются светлыми линиями на темном фоне, причем цвет линии одинаков с цветом того места сплошного спектра, которые они занимают.
Линейчатый спектр показывает, что данное вещество испускает лучи не всевозможных длин волн / хотя бы в определенных пределах, но только лучи как бы избранные по каким–то правилам или законам. В течение долгого времени ученые тщетно старались найти какие–либо закономерности в распределении спектральных линий различных элементов, т.е. найти зависимость длины l или частоты n от какого–либо параметра.
Такую зависимость установил в 1885 году Бальмер для спектра водорода. Спектр водорода в видимой части из пяти линий: красной, зеленой, синей, фиолетовой 1 и фиолетовой 2.
Бальмер эмпирически установил, что длина волны спектральных линий водорода с большой точностью определяется формулой:
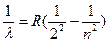 или n = cR или n = cR 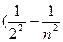 ), ),
| (2) |
где R – постоянное число, получившее название постоянной Ридберга
R= 10967758 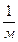 ; сR = 3, 29 × 1015 1/сек;
; сR = 3, 29 × 1015 1/сек;
n – целые числа, начиная с 3–х;
l – длина волны;
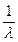 – получило название в о л н о в о е число
– получило название в о л н о в о е число 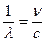 ;
;
n – частота колебаний;
С – скорость распространения света в вакууме.
Подставляя в формулу (2) n = 3 получим значение длины волны для красной линии водорода; при n = 4 – для зеленой; при n = 5 – для синей и т.д.
Ряд спектральных линий, для которых l (или n) связаны между собой одной формулой, называется серией спектральных линий, а сама формула с е р и а л ь н о й.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Серия водородных линий, определяемых формулой (2), называется серией Бальмера. Она продолжается в ультрафиолетовой части спектра. Всего в ней было найдено 29 линий (от n=3 до n=31).
Были получены и другие сериальные формулы водородных линий. В общем случае сериальная формула для водорода имеет вид:
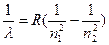 или n = сR ( или n = сR (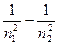 ) )
| (2/) |
Известны серии Лаймана при n1=1, для линий в ультрафиолетовой части спектра. Серия Пашена при n1 = 3, для линий в инфракрасной части спектра. Известны и другие серии при
n1 = 4, n1 = 5, n1 = 6.
Р. Ридберг показал, что в линейчатых спектрах не только водорода, но и других элементов, наблюдаются спектральные серии, причем частоты n всех линий данной серии удовлетворяют соотношение:
| n = Т (n1) – Т (n2) | (3) |
где n1 и n2 – целые числа, причем n2 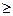 n1+1. Для данной серии n1 имеет постоянное значение. Изменение числа n дает все линии данной серии. Функции T (n1) и T (n2) называются спектральными т е р м а м и. В. Ритц установил справедливость положения названного комбинационным принципом Ритца: частоты спектральных линий излучения любого атома могут быть представлены в виде разности двух термов; составляя различные комбинации термов можно найти все возможные частоты спектральных линий этого атома. Например, беря разность термов для зеленой и красной линии водорода, получим:
n1+1. Для данной серии n1 имеет постоянное значение. Изменение числа n дает все линии данной серии. Функции T (n1) и T (n2) называются спектральными т е р м а м и. В. Ритц установил справедливость положения названного комбинационным принципом Ритца: частоты спектральных линий излучения любого атома могут быть представлены в виде разности двух термов; составляя различные комбинации термов можно найти все возможные частоты спектральных линий этого атома. Например, беря разность термов для зеленой и красной линии водорода, получим:
R (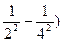 – R (
– R (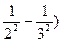 = R (
= R (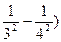
первую линию водорода серии Пашена. При неограниченном возрастании n частоты n всех серий спектра сходятся к соответствующим границам. Граничные частоты серии водородного спектра Т (n) = 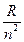 .
.
Все усилия физиков вывести сериальные формулы из общих законов электромагнитной теории света оказалась безуспешным. Не только вывод формул, но даже простое качественное описание возникновения линейчатых спектров оказалось не под силу старой классической физике, хотя предложенная Резерфордом ядерная модель строения атома и была, в основном, правильной.
|
|
