Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

ПРИМЕР #6

Задана передаточная функция системы и входной сигнал равный 1(t):

.

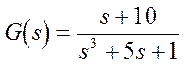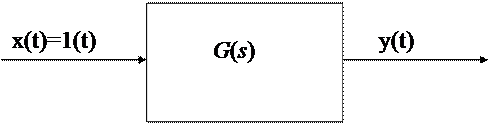Получить " конечное значение" переходной характеристики системы:

lim y (t) при t ® ¥.

Решение:

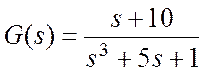
- выходной сигнал:

,

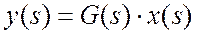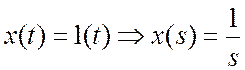
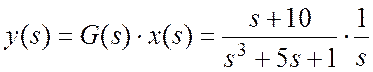
- когда y (s) уже определен, его конечное значение может быть получено взятием предела в s-области:

.

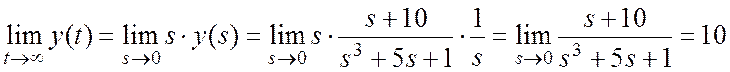
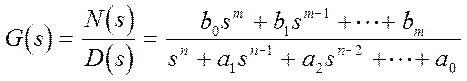
полином

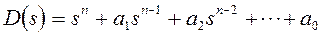
называется характеристический полином системы,

уравнение

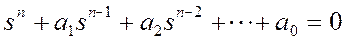
называется характеристическое уравнение equation системы.

Решение характеристического уравнения составляет действительные и/или комплексно- сопряженные числа,

.

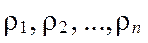Эти числа, то есть, корни характеристического уравнения называются полюса системы.

Корни числителя полинома числителя, N (s), могут быть найдены как решение уравнения

.

,

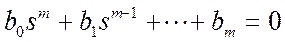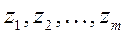и называются нулями системы.

Эти полиномы могут представлены через нули и полюса следующим образом (полюса/нули форма):

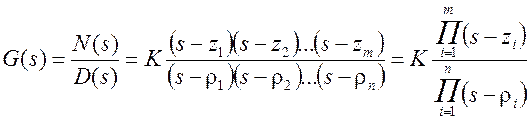(1.6)

Заметим, что коэффициент

K = b ₀,

известен как коэффициент усиления.

Алгоритм решения однородного дифференциального уравнения n-ого порядка:

,

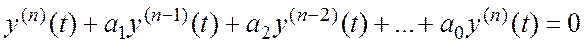начальные условия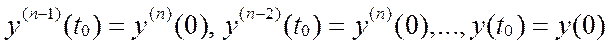

Шаг 1. Преобразование по Лапласу исходного уравнения

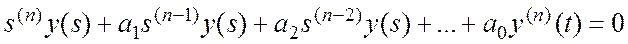
Шаг 2. Получение характеристического уравнения

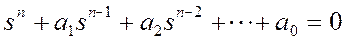
Шаг 3. Корни характеристического уравнения (полюса):

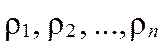
Шаг 4. Решение:

,

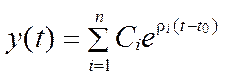где 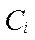- постоянные, зависят от начальных условиях.

n	Вещественные корни	Комплексные корни
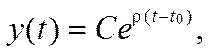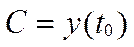
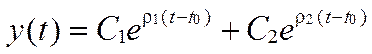
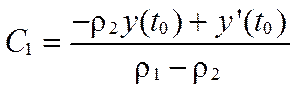
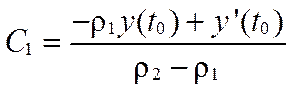
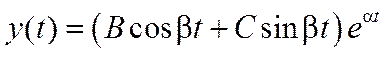
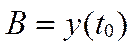