Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Результаты работы программы. C1*exp(t)+C2*exp(-t)+C3*exp(t)*t+C4*exp(-t)*t

> >

ans =

C1*exp(t)+C2*exp(-t)+C3*exp(t)*t+C4*exp(-t)*t

ans =

1/2*exp(t)-1/2*exp(-t)+1/4*exp(t)*t-1/4*exp(-t)*t

S =

y1: [1x1 sym]

y2: [1x1 sym]

y3: [1x1 sym]

y4: [1x1 sym]

ans =

1/2*exp(t)-1/2*exp(-t)+1/4*exp(t)*t-1/4*exp(-t)*t

ans =

3/4*exp(t)+1/4*exp(-t)+1/4*exp(-t)*t+1/4*exp(t)*t

ans =

-1/4*exp(-t)*t+1/4*exp(t)*t+exp(t)

ans =

1/4*exp(t)*t+5/4*exp(t)-1/4*exp(-t)+1/4*exp(-t)*t

S =

y1: [1x1 sym]

y2: [1x1 sym]

y3: [1x1 sym]

ans =

C1-C2*exp(-1/2*t)+C2*exp(1/2*t)-2*C4+C4*exp(-1/2*t)+C4*exp(1/2*t)-2*t

ans =

C5+t*C6+1/4*t^2

ans =

-2*C2+C2*exp(-1/2*t)+C2*exp(1/2*t)+C3-C4*exp(-1/2*t)+C4*exp(1/2*t)-4

S =

y1: [1x1 sym]

y2: [1x1 sym]

y3: [1x1 sym]

ans =

-2*t-2*exp(-1/2*t)+2*exp(1/2*t)

ans =

1/4*t^2

ans =

-4+2*exp(-1/2*t)+2*exp(1/2*t)

S =

y1: [1x1 sym]

y2: [1x1 sym]

y3: [1x1 sym]

y4: [1x1 sym]

y5: [1x1 sym]

y6: [1x1 sym]

ans =

-2*t-2*exp(-1/2*t)+2*exp(1/2*t)

ans =

-2+exp(-1/2*t)+exp(1/2*t)

ans =

1/4*t^2

ans =

1/2*t

ans =

-4+2*exp(-1/2*t)+2*exp(1/2*t)

ans =

-exp(-1/2*t)+exp(1/2*t)

> >

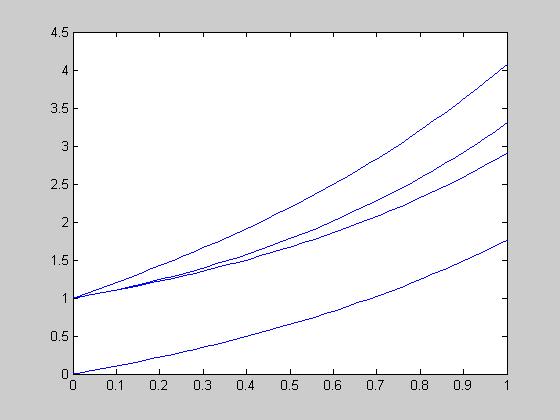
Рис.1.

Рис.2.

Варианты заданий

Задана подынтегральная функция вида:

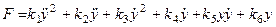, (4.1)

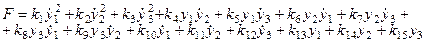, (4.2)

Значения коэффициентов заданы в табл. 1, 2.

Таблица 1

Коэффициенты функции (4.1)

Таблица 2

Коэффициенты функции (4.2)

Контрольные вопросы

1. Приведите формулировки необходимых условий экстремальности функционала.
2. Естественные граничные условия.
3. Условия трансверсальности.
4. Принцип Гамильтона.
5. Сформулируйте задачу вариационного исчисления в высших производных и метод ее решения.
6. Сформулируйте задачу вариационного исчисления для нескольких функций и метод ее решения.