Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Решение задачи для нескольких функций

Определение частных производных подынтегральной функции 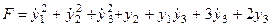функционала (2):

— для функции y ₁ (t)

; ; ;

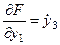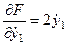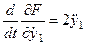— для функции y ₂ (t)

; ; ;

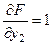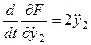— для функции y ₃ (t)

; ; .

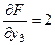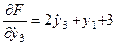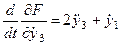Уравнения Эйлера-Лагранжа: ; ; .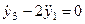

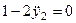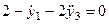Решение системы уравнений Эйлера-Лагранжа в общем виде

;

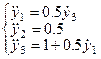а) из второго уравнения следует ;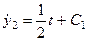

Экстремали: ;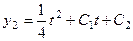

б) из первого уравнения следует 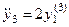, подставляем в третье уравнение и получаем ;

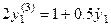характеристический многочлен —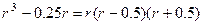

общее решение для однородного уравнения —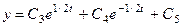

частное решение для неоднородного уравнения —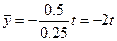

Экстремали: .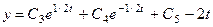

в) из третьего уравнения следует 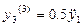; ; 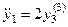; 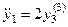подставляем в первое уравнение и получаем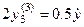

характеристический многочлен —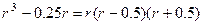

Экстремали: .

Система дифференциальных уравнений первого порядка, соответствующая полученному уравнению Эйлера-Лагранжа

.
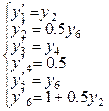