
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткие теоретические сведения. Тема работы: исследование задач вариационного исчисления с высшими производными и для нескольких функций при отыскании безусловного экстремума (программная
|
|
ЛАБОРАТОРНАЯ РАБОТА №3
Тема работы: исследование задач вариационного исчисления с высшими производными и для нескольких функций при отыскании безусловного экстремума (программная среда MATLAB).
Цель работы: изучение теории Эйлера—Лагранжа для решения вариационных задач с применением существующих пакетов прикладных программ.
Краткие теоретические сведения
Наряду с задачами для функционалов вида
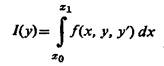
существуют также и другие постановки задач.
В качестве необходимых условий экстремума указываются только уравнения Эйлера—Лагранжа.
Задачи с высшими производными. Для задачи нахождения экстремума функционала
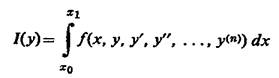
с граничными условиями
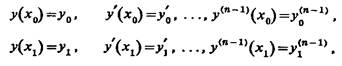
уравнение Эйлера—Лагранжа имеет вид
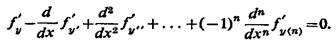
Задачи для нескольких функций. Для задачи нахождения экстремума функционала
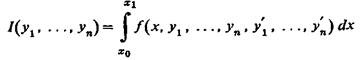
с граничными условиями
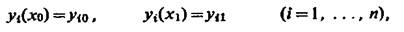
уравнение Эйлера—Лагранжа имеет вид

|
|
