💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Практика розвивального навчання

Сучасне розуміння ідей розвивального навчання підготовлене тривалими пошуками світовою педагогічною думкою шляхів і засобів навчання, які найбільшою мірою сприяють розвитку пізнавальних здібностей та особистості дитини в цілому.

Термін " розвивальне навчання" належить великому швейцарському педагогу Й.Г. Песталоцці.

Великий вклад у поширення ідей розвивального навчання внесли психологи і педагоги різних епох: К.Д.Ушинський, Л.С. Виготський, Н.О. Менчинська, Г.С. Костюк, Л.В. Заков, П.Я. Гальперін, Н.Ф. Тализіна, В.В. Давидов, Д.Б.Ельконін.

В Україні ідея розвивального навчання почала активно розроблятися у ЗО -х роках у Харківській психологічній школі. При Харківському університеті працює один із відомих науково-практичних центрів розвивального навчання під керівництвом професора О.К. Дусавицького. Відомішими на сьогодні є школи Д. Давидова-Д. Ельконіна; Л. Занкова та ін.

Розвивальне навчання - систематичний, цілеспрямований процес педагогічної взаємодії, метою якого є формування у людини тих чи інших психічних здібностей чи якостей, яких до того у неї не було.

Компоненти розвивального навчання:

1. Розвиток процесів сприймання.

2. Оволодіння всім діапазоном загально навчальних умінь і навичок.

3. Нагромадження індивідуального досвіду пошукової діяльності.

4. Розвиток уяви і літературної творчості.

5. Вправляння у комбінуванні, конструюванні, перетворенні.

6. Основний принцип організації змісту навчання - єдності навчання і виховання, який реалізується через співробітництво у навчальній та ін. діяльності.

7. Формою навчання і виховання є колективна діяльність, у межах якої одиницею спільної діяльності є групування по5-7 осіб, а клас є полем взаємозв'язку міх учнями і учителем та окремими групами.

8. Засобами навчання і виховання виступають зразки культури.

Експериментальний курс математики має такі особливості:

1) Формування у школярів передумов теоретичного мислення – основна ціль курсу математики, тому він орієнтований, у першу чергу, на формування теоретичних понять, а не тільки на вироблення практичних умінь і навичок.

2) Розгортання навчального матеріалу за принципом руху думки від загального до конкретного. Абстрактний матеріал (зокрема буквенна символіка) вводиться на самому початку навчальної роботи з якогось розділу.

3) Введення дітей у сферу відношень величин, виділення засобами певних предметних дій відношень об'єктів (більше, менше, дорівнює). Властивості величин розкриваються при оперуванні людиною реальними довжинами, об'ємами, вантажами, проміжками часу (іще до їх вираження числами). Так, уявлення про довжину діти отримують прикладаючи предмети один до одного; про площу - суміщаючи плоскі предмети один з одним; про місткість - переливаючи воду із однієї посудини в іншу і т.д.

4) Розкриття кратного відношення величин як загальної форми числа. При цьому у дітей формується поняття числа не як сукупності окремих частин, а як інструмента лічби, який дозволяє отримувати з однієї величини іншу.

5) Послідовне введення дітей в область різних видів чисел (натуральних, дробових, від'ємних), формування у них понять про ці числа як одного із проявів загального кратного відношення величин при визначених конкретних умовах.

6) Розкриття однозначності математичної операції (якщо відоме значення двох елементів операції, то за ними можливо однозначно визначити значення третього елемента) - формування у них взаємозв'язку елементів основних арифметичних дій.

7) Геометричний матеріал пов'язується з вивченням чисел і арифметичних дій. Наприклад, задача на знаходження периметра прямокутника розглядається у зв'язку з розподільним законом множення відносно суми, на уроках виконуються і власне геометричні вправи. На основі викреслювання, вирізання, моделювання діти вчаться розпізнавати геометричні фігури, знайомляться з їх властивостями.

8) При формуванні математичних понять важливу роль відіграють буквені та просторово-графічні моделі.

9) Основна функція контролю засвоєного матеріалу полягає у забезпеченні загального способу предметної дії усіма операціями, необхідними для успішного вирішення дитиною всього різноманіття конкретно-часткових задач. Наприклад, коли дитина в принципі уже володіє загальним способом вимірювання величин, отримуючи визначений результат, учитель пропонує повторити це вимірювання, змінюючи при цьому якусь конкретну операцію вимірювання з правильної на не правильну.

Подальша реалізація концепції школи розвитку особистості вимагає виконання ряду науково-дослідних проектів:

1. Розробка психолого-педагогічних основ концепції.

2. Розробка нового покоління навчальних програм та підручників.

3. Розробка психолого-педагогічної моделі педагога нового типу і методу його підготовки.

Питання для самоконтролю

1. Схарактеризуйте становлення та розвиток вітчизняної методики викладання математики в початкових класах.
2. Назвіть основні напрямки розвитку методики викладання математики за кордоном.
3. Вкажіть перспективи подальшого вдосконалення методики викладання математики в початкових класах (активізація, оптимізація, індивідуалізація, диференціація процесу навчання, інтегровані уроки, комп'ютеризація навчання тощо).
4. Схарактеризуйте основні принципи розвиваючого навчання математики.

ТЕМА№3: ПОЧАТКОВИЙ КУРС МАТЕМАТИКИ ЯК НАВЧАЛЬНИЙ ПРЕДМЕТ

ЛЕКЦІЯ З

ПЛАН

1. Освітні, виховні і розвивальні завдання математики в початкових класах.

2. Зміст початкового курсу математики та система його побудови.

3. Методика розкриття змісту початкового курсу математики: формування математичних понять, предметних і загально-предметних умінь та навичок.

4. Математична підготовка дітей у дитячому садку.

5. Наступність математичної підготовки дітей старшого дошкільного та молодшого шкільного віку, а також - молодших школярів та учнів У-VI класів.

Література А:

1. Богданович М., Козак М., Король Я. Методика викладання математики в початкових класах. - Тернопіль.: Навчальна книга - Богдан, 2001. - С. 16-29.

2. Методика начального обучения математике / Под ред. Столяра А.А и Дрозда В.Л. -Минск: Вьішейшая школа, 1988. -С. 15-31.

3. Навчання і виховання учнів 1 класу / Упор. Савченко О.Я. - К.: Початкова школа, 2002. - С. 210-298.

Б:

1. Давьідов В.В. Психологические возможности младших школьников в усвоении математики. - М.: Просвещение, 1969.

2. Мухина В.С. Шестилетний ребенок в школе. - М.: Просвещение, 1990. -С.97-99.

3. Щербакова Е.И. О математике мальїшам. - К.: Радянська школа, 1986. -72 с.

1. Освітні, виховні і розвивальні завдання математики в початкових класах

Питання освітніх виховних і розвивальних завдань навчання математики в початкових класах слід розкривати враховуючи положення сучасної концепції початкового курсу математики, спираючись на діючу програму і підручники початкової школи, програму дитячого садка, програму і посібники математики для 5-6 класів.

Зальна мета вивчення математики у початкових класах стосується розв'язання таких питань:

- здобуття учнями елементарної математичної освіти;

- підготовка до ґрунтовного вивчення матеріалу в наступних класах;

- застосування набутих знань у повсякденному житті при вивченні інших дисциплін, для розуміння повідомлень масової інформації.

Ця мета конкретизується при вивченні математики у кожному класі та на кожному уроці і є триєдиною, тобто містить навчальний (освітній), виховний, розвивальний компонент.

Освітні завдання навчання математики реалізується шляхом формування системи теоретичних знань (понять, уявлень) та практичних способів дій (умінь та навичок).

Приклад. Дидактична (навчальна) мета уроку математики може бути сфо­рмульована так: сформувати знання алгоритму письмового додавання двоциф­рових чисел без переходу через десяток, уміння застосовувати алгоритм при розв 'язуванні прикладів, продовжувати формувати уміння розв 'язувати задачі на зустрічний рух.

Виховні завдання передбачають формування світогляду, моральних, ети­чних, естетичних уявлень, поглядів, переконань дитини, мотивів діяльності, якісних рис особистості.

Приклад: формувати вольові якості особистості, наполегливість у дове­денні справи до кінця, охайність при оформленні математичних записів, само­стійність, працьовитість, повагу до праці інших людей та їй.

Розвивальні завдання містять розвиток психічних процесів дитини (сприймання, пам'ять, мислення, увага, мовлення та ін.)

Приклад 1: розвивати логічне мислення (формування умінь аналізувати, порівнювати, класифікувати, протиставляти, встановлювати взаємозв 'язки, узагальнювати та ін.); Приклад 2: розвивати творче мислення (формування уміння бачити, формулювати, розв'язувати проблему, доводити власні мірку­вання); Приклад 3: розвивати математичне мовлення.

2. Зміст початкового курсу математики та система його побудови

Зміст початкового курсу математики визначається цілями навчання мі­стить такі компоненти:

1. Арифметичний матеріал; 3. Алгебраїчний матеріал

2. Геометричний матеріал;; 4. Величини;

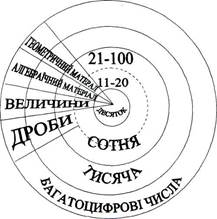
Арифметичний матеріал становить основу курсу математики, побудова­ний за концентричним принципом (виділяють концентри чисел: десяток, сотня, тисяча, багатоцифрові числа), усі інші компоненти включаються в систему арифметичних знань (рисі).

Рис. 1

Зміст арифметичного матеріалу: лічба, нумерація, чотири арифметичні дії над цілими невід'ємними числами, властивості натурального ряду чисел і ари­фметичних дій, звичайні дроби.

Геометрична пропедевтика передбачає засвоєння знань плоских геомет­ричних фігур (точка, пряма, відрізок, многокутник: трикутник, чотирикутник, прямокутник, квадрат), коло і круг), уявлень про просторові тіла (призма, піра­міда, циліндр, конус, куля) та формування умінь побудови і вимірювання відрі­зків, деяких плоских фігур.

Алгебраїчний матеріал засвоюється шляхом ознайомлення зі змінною, рі­вністю, нерівністю, рівнянням, нерівністю зі змінною, числовим виразом, фун­кціональною залежністю.

Молодші школярі оволодівають уявленнями про величини: довжину, площу, час, масу, місткість, вартість, одиниці їх вимірювання та уміннями їх вимірювання.

3. Методика розкриття змісту початкового курсу математики: формування математичних понять, предметних і загально-предметних умінь та навичок

Зміст початкового курсу математики засвоюється учнями початкових класів у вигляді знань та умінь, обсяг і рівень яких визначені програмою мате­матики 1-4 класів.

Знання - це результат пізнавальної діяльності, що виражається вигляді понять, уявлень, суджень, умовиводів, концепцій, теорій.

Поняття - одна з форм мислення, у якій відображаються загальні істотні властивості предметів і явищ об'єктивної дійсності, загальні взаємозв'язки між ними у вигляді цілісної сукупності ознак.

Ознаки, які включаються в поняття, становлять його зміст. Кількість предметів чи явищ, охоплених поняттям становить об 'єм поняття.

Поняття позначають терміном, але у початковій школі на уроці матема­тики їх розглядають у реальних життєвих ситуаціях і вводяться описово, пере­важно без чітких означень. Математична поняттєва термінологія початкової школи незначна за кількістю: чотирикутник, прямокутник, квадрат, рівняння та ін.

Уміння - здатність належно виконувати певні дії, заснована на доцільно­му використанні людиною набутих знань і навичок.

Формування умінь - складний процес аналітико-синтетичної діяльності, він проходить такі стадії:

- ознайомлення з умінням, усвідомлення його смислу (засвоєння знань про
спосіб і послідовність виконання дій);

- виконання дій за зразком;

- виконання дій в подібній ситуації;

- виконання дій в новій ситуації.

Навички - дії доведені до ступеню автоматизму.

На уроці математики формують уміння: загально предметні та власне предметні.

Загально предметні уміння формуються на усіх уроках початкової школи: організаційні (уміння планувати свою діяльність, користуватися підручником); загально-пізнавальні (спостерігати, міркувати, відтворювати); мовленнєві (слу­хати, висловлювати свою думку); контрольно-оцінні (навички самоконтролю, самооцінки).

Власне предметні уміння формуються виключно на уроках математики: уміння розв'язувати задачі, уміння будувати і вимірювати відрізки, навички швидкої усної лічби і т. д.

4. Математична підготовка дітей у дитячому садку

У програмі з математики для дитячих садків виділяють такі групи уяв­лень: кількісна оцінка величин, числові поняття, поняття про форму, вимірю­вання, поділ цілого на частини, орієнтування в просторі.

Кількісна оцінка величин: більший, менший, однаковий за величиною; вищий, нижчий, однаковий за висотою; довший, коротший, однаковий за дов­жиною; ширший, вужчий, однаковий за шириною; товщий, тонший, однаковий за товщиною; важчий, легший.

Числові уявлення: діти вчаться лічити предмети, називати числа у зворо­тному порядку, розуміти кількісне й порядкове значення числа, називати склад числа з двох менших.

Уявлення про форму( геометричні фігури): круг, трикутник, чотирикут­ник, квадрат, брус, піраміда, куб, куля, циліндр.

Вимірювання: поняття „міра" (умовна міра довжини, сипких речовин).

Ознайомлення з природними одиницями часу (рік і пори року, місяць, тиждень, доба) та з циферблатом годинника.

5. Наступність математичної підготовки дітей старшого дошкільного та молодшого шкільного віку, а також - молодших школярів та учнів У-УІ класів.

Принцип наступності є одним з основних дидактичних принципів. Він передбачає встановлення тісних зв'язків між різними ланками освіти, зокрема, між дошкіллям та початковою школою і між початковою школою та 5-6 класа­ми. Цей принцип вимагає узгодженості у цілях, змісті, організаційно-методичному забезпеченні етапів освіти, які межують один з одним: дошкілля -початкова школа - основна школа.

Для забезпечення наступності в математичній підготовці дітей старшого дошкільного та молодшого шкільного віку вчитель повинен ознайомитися з яким обсягом знань приходять до школи шестилітні діти.

Обсяг знань дошкільника досить великий, та ці знання формуються на рі­вні первинних уявлень і тому потребують подальшого уточнення та системати­зації.

У 1 класі вивчення математики продовжується за тими ж змістовими ліні­ями, що й у дошкіллі, та дублювання змісту не відбувається, він розширюється й поглиблюється, діти отримують крім емпіричних і теоретичні знання, вчаться застосовувати їх у своїй діяльності.

Для успішного переходу мислительної діяльності учнів від конкретно-образної до абстрактної необхідно при первинному формуванні понять здійс­нювати систематизацію чуттєвого досвіду. Для цього у організації навчання першокласників математики доцільно використовувати крім уроку й інші фор­ми, наприклад, екскурсії у природу.

При виборі методів навчання 6-літніх дітей застосовують відомі словесні, практичні, наочні методи навчання, але перевагу надають практичним та емо­ційно-стимулюючим, спостереженню та грі.

Наступності і поетапності потребує також використання унаочнення та роздаткового матеріалу: у перші місяці навчання переважає предметна наоч­ність далі використовують силуетні зображення та малюнки, пізніше перехо­дять до схематичного унаочнення. Особливо емоційно сприймають першоклас­ники словесну наочність: опис вчителем предметів, художні твори, усну народ­ну творчість, лічилки.

Важливою умовою успішного навчання та забезпеченням наступності (ДС-ІШІ) є індивідуалізація навчання, адже діти не достатньо навчені працюва­ти самостійно, не вміють читати, їм важко запам'ятати інструкцію вчителя і працювати за нею, важко виконувати одноманітну роботу тривалий час. поси­льними завданнями є ті, у яких необхідно відповідь подати графічно (обвести, з'єднати, домалювати, розфарбувати).

Отже, забезпечення наступності в організації математично підготовки ді­тей старшого дошкільного та молодшого шкільного віку має здійснюватися ці­леспрямовано і багатопланово. Воно передбачає продовження формування чут­тєвого досвіду дітей, застосування в роботі тих методів, прийомів, форм органі­зації навчання, які знайомі й звичні для них ще з дошкільного дитинства.

Вивчення математики в 5-6 класах базується на тій математичній підгото­вці, яку учні дістали в початковій школі. В цілому вона визначена тими вимо­гами, що зазначені в програмі для учнів на кінець четвертого року навчання.

Мета засвоєння курсу математики 5-6 класів - систематизація знань про розвиток поняття числа та вироблення вмінь виконувати усно і письмово ариф­метичні дії над числами, перекладати практичні задачі на мову математики, підготовка учнів до вивчення систематичних курсів алгебри й геометрії.

Курс базується на індуктивній основі із залученням елементів дедуктив­них міркувань.

Програма з математики для учнів 5-6 класів містить три розділи: арифме­тика, елементи алгебри, елементи геометрії. Розділ арифметики можна назвати основним, як і в початковій школі, а останні два - пропедевтичними.

Вчителі початкових класів повинні враховувати перспективи навчання в 5-6 класах. З цього погляду треба знати не лише основні напрямки розгортання матеріалу, а й враховувати межі їх розвитку, тобто завершеність певної ідеї та очікувані результати.

Запитання для самоконтролю

1. Назвіть освітні, виховні і розвивальні завдання математики в початкових класах.

2. Схарактеризуйте зміст початкового курсу математики та систему його побудови.

3. Опишіть методику розкриття змісту початкового курсу математики: формування математичних понять, предметних і загально-предметних умінь та навичок.

4. Схарактеризуйте математичну підготовку дітей у дитячому садку.

5. У чому полягає наступність математичної підготовки дітей старшого дошкільного та молодшого шкільного віку, а також - молодших школярів та учнів У-VI класів.