Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Методы определения масс небесных тел.

Закон всемирного тяготения Ньютона позволяет измерить одну из важнейших физических характеристик небесного тела - его массу.

Массу можно определить:

а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ),

б) по третьему уточнённому закону Кеплера,

в) из анализа наблюдаемых возмущений, производимых небесным телом в движениях других небесных тел.

1. Первый способ применяется на Земле.

На основании закона тяготения ускорение g на поверхности Земли:

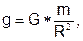где m - масса Земли, а R - её радиус.

m = (gR2)/G.

g и R измеряются на поверхности Земли. G = const.

С принятыми сейчас значениями g, R, G получается масса Земли:

m = 5, 976.1027г = 6.1024кг.

Зная массу и объём, можно найти среднюю плотность. Она равна 5, 5 г/см3.

2. По третьему закону Кеплера можно определить соотношение между массой планеты и массой Солнца, если у планеты есть хотя бы один спутник и известны его расстояние от планеты и период обращения вокруг неё.

где M, m, mc- массы Солнца, планеты и её спутника, T и tc- периоды обращений планеты вокруг Солнца и спутника вокруг планеты, а и ас - расстояния планеты от Солнца и спутника от планеты соответственно.

Из уравнения следует

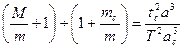
Отношение М/m для всех планет очень велико; отношение же m/mc, очень мало (кроме Земли и Луны, Плутона и Харона) и им можно пренебречь.

Соотношение М/m можно легко найти из уравнения.

Для случая Земли и Луны нужно сначала определить массу Луны. Это сделать очень сложно. Решается задача путём анализа возмущений в движении Земли, которые вызывает Луна.

3. По точным определениям видимых положений Солнца в его долготе были обнаружены изменения с месячным периодом, называемые " лунным неравенством". Наличие этого факта в видимом движении Солнца указывает на то, что центр Земли описывает небольшой эллипс в течение месяца вокруг общего центра масс " Земля - Луна", расположенного внутри Земли, на расстоянии 4650 км. от центра Земли.

Положение центра масс Земля-Луна было найдено также из наблюдений малой планеты Эрос в 1930 - 1931 гг.

По возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось 1/81, 30.

В 1964 году Международный астрономический союз принял его как const.

Из уравнения Кеплера получаем для Солнца массу = 2.1033г., что в 333000 раза превосходит земную.

Массы планет, не имеющих спутников, определены по возмущениям, которые они вызывают в движении Земли, Марса, астероидов, комет, по возмущениям, производимым ими друг на друга.