Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Булевы функции.
|
|
Изучить по учебной литературе вопросы:
3.1. Понятие булева вектора и булевой функции.
3.2. Способы задания булевой функции.
3.3. Приведение функции к совершенной ДНФ.
3.4. Приведение функции к совершенной КНФ.
3.5. Минимизация булевой функции. Метод карт Карно.
3.6. Двоичное сложение. Полином Жегалкина.
Примеры решения задач рассмотрены на третьем и четвертом обзорных установочных занятиях.
Пример 1:
Задать формулой функцию f (
; 
; 
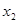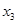), имеющую таблицу истинности:
| Таблица истинности | ||||
|
|
|
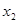
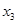
| f (; ; )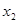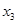
| |
Решение: для наборов значений переменных (1; 1; 0), (1; 0; 1), (0; 1; 0), (0; 0; 0), на которых функция принимает значение 1, запишем конъюнкции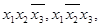 
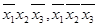(см. таблицу 4), а искомая формула имеет вид:
f (; ; )= 
.
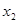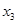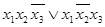
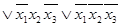Пример 2:
Найти формулу, определяющую функцию f (x; y; z), по заданной таблице истинности. Упростить полученную формулу.
| Таблица истинности | |||
| х | y | z | f (х; y; z) |
Решение: используя правило получения формулы из таблицы истинности для функции f (x; y; z), имеем: f (x; y; z) =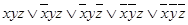 
.
Упрощаем полученную формулу, используя формулы логики:
f (x; y; z) =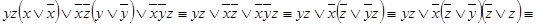 
.
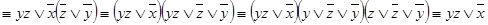Таким образом, f (x; y; z) =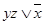 
.
Пример 3. Привести функцию f (x; y; z) =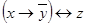 
к ДНФ.
Решение:
f (x; y; z) =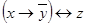 
.
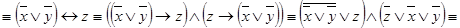
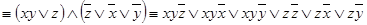Функция f (x; y; z) уже записана в виде ДНФ. Но её можно упростить:
f (x; y; z) =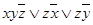 
.
Пример 4. Найти СДНФ для функции f (x; y; z) =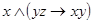 
.
Решение:
1) ищем ДНФ для данной функции:
f (x; y; z) =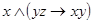 
;
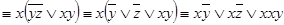2) конъюнкция xxy содержит переменную x дважды, поэтому используем равносильность x 
x ≡ x:
f (x; y; z) =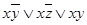 
;
3) элементарные конъюнкции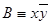 
и С ≡ xy не содержат переменной z, а элементарная конъюнкция 
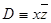не содержит переменной y, поэтому используем равносильности 
, 
, 
:
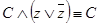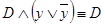f (x; y; z) =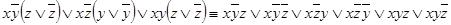 
;
4) теперь ДНФ содержит две одинаковые элементарные конъюнкции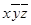 
и две одинаковые элементарные конъюнкции 
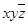, поэтому лишние отбрасываем, используя равносильности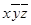 
≡ , ≡ :
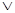
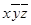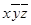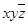
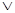
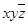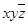f (x; y; z) =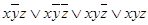 
.
Таким образом, функция f (x; y; z) записана в виде ДНФ.
Пример 5. Дана функция f (x; y; z) = 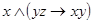. Записать её в виде СДНФ путём составления таблицы истинности.
Решение: составляем таблицу истинности:
| х | y | z | yz | xy | yz → xy | f (x; y; z) |
Тогда СДНФ для данной функции будет выглядеть так:
f (x; y; z) =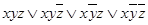 
. 10
Пример 6. Метод Карно.
|
 00
| |
По карте можно составить СДНФ и СКНФ, как по таблице истинности. Мы показали, какие наборы соответствуют каждой ячейке. Для задания функции по карте в ячейке указывается значение функции на данномнаборе. Необходимо составить СДНФ:
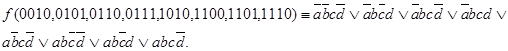
Минимизируем функцию с помощью карты.
  0
|  
  1
|   0
|
 0
| ||||||||
     0
| 1 |  1
|  1
| ||||||||
| 1 | 0 | 1 | ||||||||
   0
|  1
|  0
| 0 |
|
|
Получим ДНФ: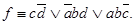 
Пример 7. Представить функцию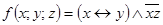 
в виде полинома Жегалкина.
Решение:
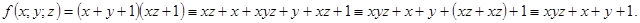Пример 8. Представить функцию 
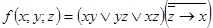в виде полинома Жегалкина. Решение:
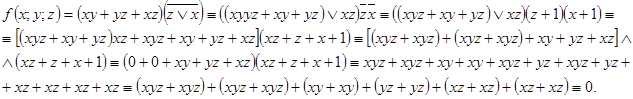
После изучения теории и решения примеров по данной теме можно решить задание №4 и №5 контрольной работы.
|
|