💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Основы теории множеств.

Изучить по учебной литературе вопросы:

1.1. Основные понятия теории множеств.

1.2. Задание множеств.

1.3. Операции над множествами.

1.4. Свойства операций.

1.5. Декартово произведение.

Примеры решения задач рассмотрены на первом обзорном установочном занятии.

Пример 1: Пусть А ={1; 7; 3}, тогда: 5 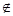А (или 5 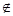{1; 7; 3}); 3Î А.

Пример 2: Пусть А={1; 2; 3}. Множества {1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3} являются собственными подмножествами множества А. Множества {1; 2; 3}и Ø являются несобственными подмножествами множества А.

Пример 3: А={1; 2; 3; 4}, B={2; 4; 6}; ;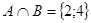

Пример 4: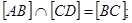

Пример 5: ;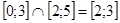

Пример 6: ;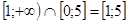

Пример 7: (-¥; 0)Ç [-5; -3]=[-5; -3];

Пример 8: 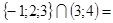Æ;

Пример 9: ;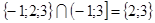

Пример 10: В={2n: nÎ N }, A= N; АÇ В=В; следует обратить внимание, что если ВÌ А, то АÇ В=В.

Пример 11: {1; 2; 3}È {4; 5}={1; 2; 3; 4; 5}.

Пример 12: {1; 2; 3}È {3; 4}={1; 2; 3; 4}.

Пример 13: А={1; 2; 3; 4}, B={1; 2}; A\B={3; 4};

Пример 14: A={1; 2; 3}, B={3; 4; 5; 6}; A\B={1; 2};

Пример 15: A={1; 2; 5}, B={3; 4}; A\B={1; 2; 5};

Пример 16: A={1; 2}, B={1; 2; 3}; A\B=Æ;

Пример 17: [0; 3]\[2; 5]=[0; 2);

Пример 18: {-1; 2; 3}\ (2; 3)= {-1; 2; 3};

Пример 19: {-1; 2; 3}\ [-1; 3)={3}.

Пример20: Пусть Y={1; 2; 3; 4; 5}, тогда: 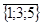={2; 4}.

Пример21: Пусть Y=(-¥; +¥), тогда:

[2; 3)=(-¥; 2)È [3; +¥); (-¥; -7]=(-7; + ¥).

Пример21: А={0; 1}, B={2; 3}; A´ B={(0; 2); (0; 3); (1; 2); (1; 3)}.

После изучения теории и решения примеров по данной теме можно решить задание №1 контрольной работы.