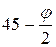Давление грунтов на подпорные стенки
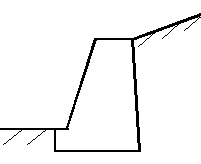
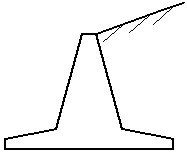
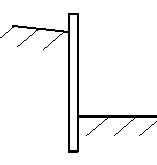
Подпорная стенка удерживает массив грунта от обрушения. Различают гравитационные и шпунтовые подпорные стенки (рис. 4.7).
| 
| 
| | Рис. 4.7.
а, б – гравитационные подпорные стенки, массивная (а) и тонкоэлементная (б);
в – шпунтовая стенка
|
Основной нагрузкой для них является боковое давление грунта. Как подпорные стенки работают также стены подвалов зданий и подземных сооружений.
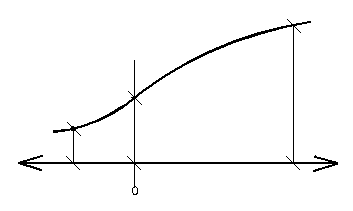
В зависимости от величины и направления возможного смещения стенки на нее может действовать давление покоя, активное (распор) или пассивное давление (отпор). Активное давление возникает даже при небольших смещениях стенки от грунта засыпки; пассивное – при значительных смещениях стенки на засыпку. В обоих случаях грунт приходит в предельное состояние с формированием призмы обрушения (при активном) и призмы выпора при пассивном давлении. График изменения давления в зависимости от перемещения стенки показан на рис. 4.8.
Здесь нужно рассмотреть только давление для состояний предельного равновесия грунта. В состоянии покоя, когда нет боковых смещений, значение коэффициента бокового давления определяется формулой (2.3).
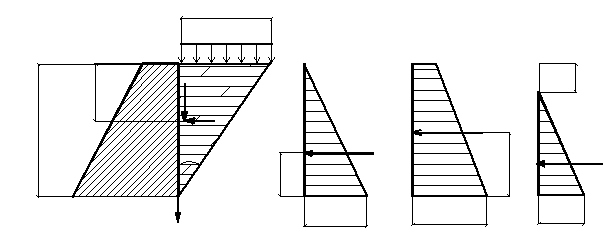
Ограничиваемся рассмотрением гладкой вертикальной стенки с горизонтальной засыпкой (рис. 4.9).
Пусть стенка имеет высоту h, засыпка представлена песком (φ ≠ 0; с=0). Рассмотрим напряжения в точке задней грани стенки на глубине z.
Поскольку стенка гладкая, вертикальное и горизонтальное напряжения в точке – главные, причем большее главное напряжение σ z = σ 1 = γ z, а меньшее горизонтальное является активным давлением и равно: σ а=σ х=σ 3=λ аσ 1=λ аγ z, где 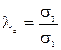 – коэффициент активного бокового давления. Значение коэффициента λ а следует из УПР (2.17): – коэффициент активного бокового давления. Значение коэффициента λ а следует из УПР (2.17):
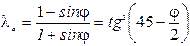 . (4.14) . (4.14)
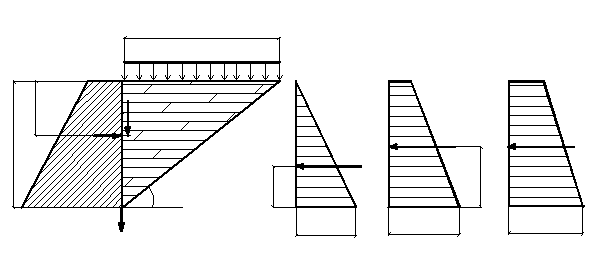
Эпюра изменения σ по высоте приведена на рис. 4.9 а. Равнодействующая активного давления равна площади треугольника и выражается формулой:
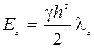 . (4.15) . (4.15)
Пусть на поверхности засыпки действует равномерно распределенная нагрузка q. В этом случае эпюра активного давления трапецеидальная и равнодействующая или площадь эпюры (рис. 4.9, б) равна:
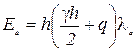 . (4.16) . (4.16)
Рассмотрим учет сцепления грунта при определении активного давления. Ранее было установлено, что на высоту hкр по (4.11) связный грунт держит вертикальный откос. Считаем, что до этой глубины грунт не оказывает давления на стенку. Таким образом, эпюра начнется в точке на глубине hкр от верха стенки (рис. 4.9b). Нижняя ордината эпюры определится из УПР (2.16)
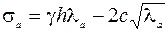 . .
Равнодействующая давления равна:
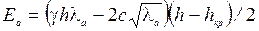 . (4.17) . (4.17)
Таким образом, учет сцепления уменьшает активное давление. В формулах (4.15 – 4.17) Еа измеряется в кН/м, т.е. давление устанавливается на единицу длины стенки.
Пассивное давление возникает при смещении стенки на засыпку. При этом напряжение σ z = σ 3 минимальное, а σ x = σ 1 = σ p максимальное, то есть является пассивным давлением.
При этом из УПР (2.16) в точке 0≤ z ≤ h получаем
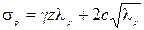 , (4.18) , (4.18)
где 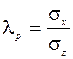 - коэффициент пассивного бокового давления, равный: - коэффициент пассивного бокового давления, равный:
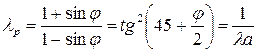 . (4.19) . (4.19)
С помощью выражения (4.18) построены эпюры пассивного давления (рис. 4.10): а – при с=0, q=0; б – при с=0, q≠ 0; b – при q=0, с≠ 0. Для получения формул равнодействующих пассивного давления достаточно записать площади эпюр. Очевидно, для случаев а и б справедливы формулы (4.15) и (4.16) с заменой λ а на λ р по (4.19). Для грунта со сцеплением эпюра пассивного давления трапецеидальная, т.е. здесь учет сцепления увеличивает давление:
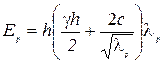 . (4.20) . (4.20)
Следует также отметить различие в размерах призм обрушения и выпора (рис. 4.10 и 4.11):
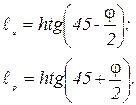 (4.21) (4.21)
В обоих случаях угол между направлением большего напряжения σ 1 и плоскостью скольжения (обрушения или выпора) равен π /4 – φ /2, как это было указано для стабилометрических испытаний.
|




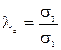 – коэффициент активного бокового давления. Значение коэффициента λ а следует из УПР (2.17):
– коэффициент активного бокового давления. Значение коэффициента λ а следует из УПР (2.17):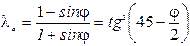 . (4.14)
. (4.14)
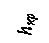
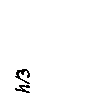

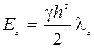 . (4.15)
. (4.15)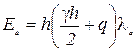 . (4.16)
. (4.16)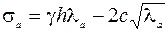 .
.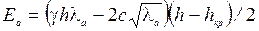 . (4.17)
. (4.17)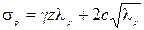 , (4.18)
, (4.18)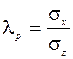 - коэффициент пассивного бокового давления, равный:
- коэффициент пассивного бокового давления, равный: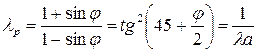 . (4.19)
. (4.19)

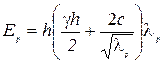 . (4.20)
. (4.20)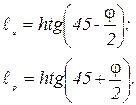 (4.21)
(4.21)