Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Вырожденные задачи наименьших квадратов

До сих пор при инимизации функции 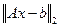предполагалось, что - матрица полного ранга. Что произойдет, если ранг матрицы не полон или же близка к матрице неполного ранга? Такие задачи возникают во многих реальных ситуациях, например, при выделении сигнала из зашумленных данных, решении некоторых типов интегральных уравнений, цифровом восстановлении изображений и т.д. эти задачи часто плохо обусловлены и чтобы превратить их в хорошо обусловленные, приходится накладывать дополнительные ограничения на их решения. Превращение плохо обусловленной задачи в хорошо обусловленную путем наложения дополнительных условий на решение называется регуляризацией.

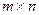Теорема. Пусть - матрица размера , причем 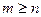и пусть ранг 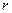матрицы меньше 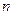. Тогда множество векторов 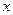, минимизирующих 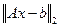, образуют 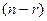-мерное линейное подпространство.

Данная теорема говорит о том, что для матрицы , имеющей (в точной арифметике) неполный ранг, решение задачи наименьших квадратов не единственно.

Вследствие ошибок в элементах матрицы или округлений при вычислениях у , как правило, не будет сингулярных чисел, в точности равных 0, но будут одно или несколько очень малых сингулярных чисел (т.е. будет близка к матрице неполного ранга). Можно показать, что единственное решение задачи наименьших квадратов вэтом случае будет очень велико и обязательно является очень чувствительным к погрешностям в 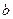. Регуляризация задачи осуществляется путем наложения некоторых условий на решение.