
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сжатие данных с помощью сингулярного разложения матрицы
|
|
Пусть для матрицы  имеется сингулярное разложение
имеется сингулярное разложение 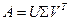 .
.
Теорема. Если 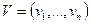 , где
, где 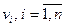 , - столбцы матрицы
, - столбцы матрицы 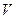 , а
, а 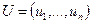 , где
, где 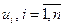 , - столбцы матрицы
, - столбцы матрицы 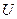 , сингулярное разложение матрицы
, сингулярное разложение матрицы  можно представить в форме внешних произведений:
можно представить в форме внешних произведений:
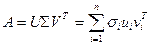 ,
,
т.е. в виде суммы матриц 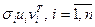 , ранга 1. Тогда ближайшая к
, ранга 1. Тогда ближайшая к  (в смысле спектральной матричной нормы
(в смысле спектральной матричной нормы 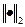 ) матрицей ранга
) матрицей ранга 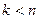 является матрица
является матрица
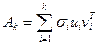 ,
,
называемая малоранговой аппроксимацией матрицы  (или аппроксимацией матрицы
(или аппроксимацией матрицы  ранга
ранга 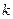 ), причем
), причем
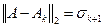 .
.
Для матрицы 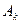 справедливо также представление
справедливо также представление
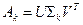 ,
,
где 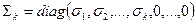 .
.
Приведенная теорема используется для сжатия изображений. Изображение размера 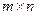 - это попросту
- это попросту 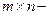 матрица, элемент
матрица, элемент  которой интерпретируется как яркость точки (пикселя)
которой интерпретируется как яркость точки (пикселя)  . Другими словами, элементы матрицы, изменяющиеся от 0 до 255, интерпретируются как точки с окраской от черной (что соответствует 0) до белой (что соответствует 255) с различными промежуточными степенями серого цвета (возможны и цветные изображения, тогда там будут фигурировать 3 матрицы). Вместо того, чтобы хранить или передавать все
. Другими словами, элементы матрицы, изменяющиеся от 0 до 255, интерпретируются как точки с окраской от черной (что соответствует 0) до белой (что соответствует 255) с различными промежуточными степенями серого цвета (возможны и цветные изображения, тогда там будут фигурировать 3 матрицы). Вместо того, чтобы хранить или передавать все 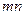 элементов матрицы, представляющей изображение, часто бывает предпочтительным сжатие этого изображения, т.е. хранение гораздо меньшего массива чисел, с помощью которых исходный образ все же может быть приближенно восстановлен. Проиллюстрируем это на примере изображения размером
элементов матрицы, представляющей изображение, часто бывает предпочтительным сжатие этого изображения, т.е. хранение гораздо меньшего массива чисел, с помощью которых исходный образ все же может быть приближенно восстановлен. Проиллюстрируем это на примере изображения размером 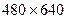 (рис.1), матрицу которого обозначим
(рис.1), матрицу которого обозначим  . При построении сингулярного разложения матрицы
. При построении сингулярного разложения матрицы 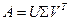 этого изображения будет вычислено 480 СНЧ. Согласно предыдущей теоремы матрица
этого изображения будет вычислено 480 СНЧ. Согласно предыдущей теоремы матрица 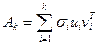 есть наилучшее приближение ранга
есть наилучшее приближение ранга 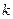 матрицы
матрицы  в том смысле, что она реализует минимум
в том смысле, что она реализует минимум 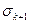 величины
величины 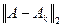 . Заметим, что для восстановления матрицы
. Заметим, что для восстановления матрицы 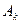 требуется лишь
требуется лишь 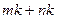 слов памяти, в которых хранятся
слов памяти, в которых хранятся 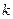 векторов
векторов 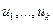 длины
длины 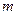 и
и 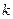 векторов
векторов 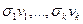 длины
длины 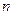 . В то же время дляхранения
. В то же время дляхранения  (или той же матрицы
(или той же матрицы 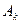 , но в явном виде) нужны
, но в явном виде) нужны 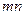 слов, т.е. гораздо большая память при малом
слов, т.е. гораздо большая память при малом 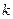 . Будем рассматривать
. Будем рассматривать 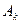 как сжатое изображение, хранимое с помощью
как сжатое изображение, хранимое с помощью  слов памяти. Эти приближенные изображения для различных значений
слов памяти. Эти приближенные изображения для различных значений 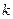 приведены на рис.2, 3. Выигрыш в памяти здесь составит
приведены на рис.2, 3. Выигрыш в памяти здесь составит 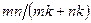 . Результаты эксперимента приведены в табл.1.
. Результаты эксперимента приведены в табл.1.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Таблица 1 -
Коэффициент 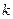 малоранговой аппроксимации малоранговой аппроксимации
| Выигрыш в памяти 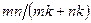 при использовании малоранговой аппроксимации при использовании малоранговой аппроксимации
|
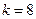
| 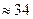
|
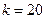
| 
|
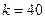
| 
|
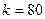
| 
|
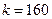
| 
|

Рис.1. Исходное изображение

Рис. 2. Сжатое изображение. Ранг аппроксимации равен 20

Рис. 3. Сжатое изображение. Ранг аппроксимации равен 160
|
|
