Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Задача наименьших квадратов. Решение линейной задачи наименьших квадратов с помощью сингулярного разложения матрицы

Лекция 30.Использование сингулярного разложения матрицы для решения различных задач

План

Задача наименьших квадратов. Решение линейной задачи наименьших квадратов с помощью сингулярного разложения матрицы

Сжатие данных с помощью сингулярного разложения матрицы

Вырожденные задачи наименьших квадратов

Задача наименьших квадратов. Решение линейной задачи наименьших квадратов с помощью сингулярного разложения матрицы

Пусть даны 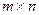-матрица и 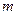-вектор 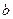. Линейная задача наименьших квадратов заключается в отыскании 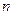-вектора 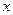, минимизирующего величину 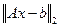(евклидова норма вектора 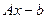). Если 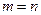и матрица невырожденная, то решением задачи является вектор 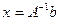(т.е. решение СЛАУ 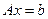). Если 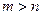, т.е. число уравнений больше числа неизвестных, то задача называется переопределенной; в этом случае, ввобще говоря, не существует вектора 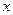, точно удовлетворяющего системе 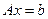. Иногда встречаются и недоопределенные задачи, где .

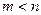Пример. Аппроксимация данных является традиционным приложением метода наименьших квадратов. Пусть даны 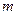пар чисел 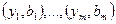. Предположим, что мы хотим найти кубический полином, который бы «наилучшим образом» представлял числа 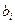как функцию от 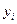. Это означает, что коэффициенты многочлена третьей степени 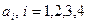, нужно определить так, чтобы многочлен

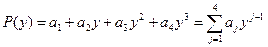
минимизировал невязку 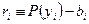для 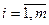, т.е. перед нами стоит задача минимизации вектора

,

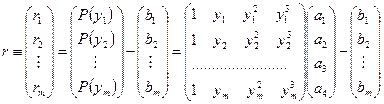где 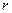и 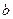- векторы длины 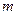, - матрица размера , а 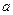- вектор длины 4. Для минимизации 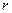можно выбрать любую норму, например, 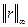, 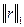или 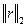. В последнем случае получаем задачу наименьших квадратов, она соответствует минимизации сумм квадратов невязок: .

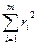Пример. В статистическом моделировании часто приходится оценивать некоторые параметры 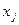, основываясь на наблюдениях, «загрязненных» шумом. Предположим, например, что в рамках компании по приему в университет желательно предсказать средний бал 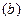будущего обучения в нем, исходя из среднего бала 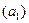, который абитуриент имел в старших классах школы, и результатов двух экзаменов (тестов): устного 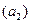и письменного 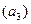. Основываясь на прошлых данных для ранее принятых студентов, можно построить линейную модель вида

.

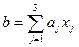Наблюдениями являются четверки чисел 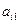, , 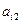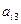и 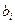, по одной для каждого из 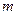студентов в базе данных. Итак, желательно минимизировать величину

,

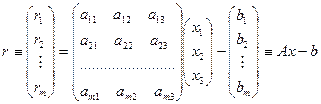что можно рассматривать как задачу наименьших квадратов.

Рассмотрим решение задачи наименьших квадратов при помощи сингулярного разложения матрицы.

Напомним, что спектральная матричная норма матрицы опрелеляется следующим образом:

,

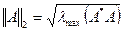где символ 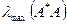обозначает максимольное собственное значение матрицы 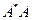. Если матрица - вещественная симметричная, то 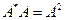, и тогда

.

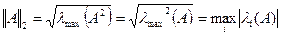Утверждение 1. Для спектральной матричной нормы верно равенство

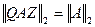, (1)

где 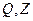- любые ортогональные матрицы.

Можно показать, что если - невырожденная матрица с сингулярным разложением 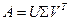, то решением задачи минимизации 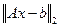является вектор

.

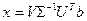Действительно:

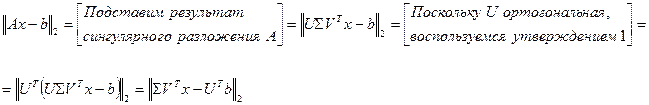
Обозначим в последнем выражении: 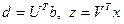, тогда получим:

.

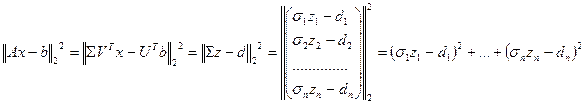Минимальное значение 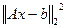, а значит и 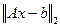достигает тогда, когда все неотрицательные слагаемые в правой части последнего равенства равны 0:

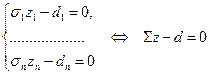(2)

Поскольку - невырожденная матрица, у нее нет нулевых сингулярных чисел, это значит, что мы можем однозначно определить из (2) :

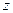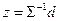. (3)

Подставим в (3) выражения 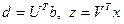, получим:

,

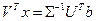откуда 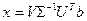, что и требовалось доказать.