Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Связь между сингулярным и спектральным разложениями матрицы

Сингулярное разложение матрицы 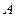общего вида тесно связано со спектральными разложениями симметричных матриц

, , .

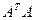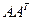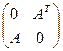Рассмотрим эту связь подробно.

Утверждение 1. Пусть 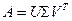есть сингулярное разложение 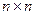-матрицы 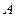в соответствии с (1). Если 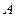симметричная матрица с СЗ 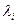и СВ 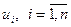, т.е. 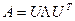есть спектральное разложение 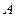, то в сингулярном разложении матрицы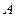 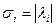, , 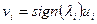причем .

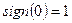Утверждение 2. Пусть 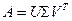есть сингулярное разложение 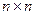-матрицы 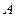в соответствии с (1). Собственными значениями симметричной матрицы 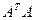являются 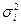, а правые СНВ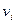 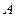— ортонормированные СВ .

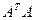Доказательство. Для матрицы 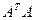имеет место соотношение:

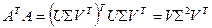. (2)

Равенство (2) очевидно представляет спектральное разложение матрицы 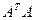, причем 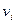— ее СВ, а диагональные элементы 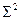— СЗ.

Утверждение 3. Пусть 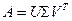есть сингулярное разложение 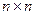-матрицы 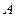в соответствии с (1). Собственными значениями симметричной матрицы 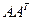являются 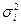. Левые СНВ 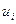— ортонормированные СВ 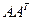, соответствующие СЗ .

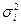Доказательство. Аналогично доказательству утверждения 2.

Утверждение 4. Пусть 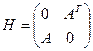, где 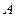— квадратная 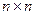-матрица, причем 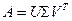есть сингулярное разложение 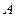в соответствии с (1). Тогда 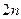СЗ матрицы 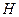— это числа 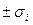, а соответствующие нормированные СВ имеют вид .

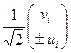Доказательство. Поскольку матрица 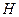симметричная, то

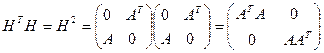. (3)

Из (3) вытекает, что 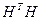— блочно-диагональная матрица, а значит ее спектр является объединением спектров блоков. Спектры блоков 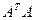, 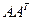— это 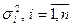. Обозначим спектральное разложение матрицы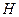

.

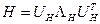Поскольку

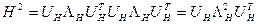, (4)

т.е. (4) — спектральное разложение 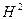, то СЗ 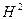— это квадраты СЗ 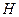, а значит 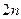СЗ 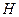определяются как 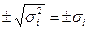, и первая часть утверждения доказана.

Для доказательства второй части проверим непосредственно, что вектор 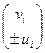является СВ матрицы :

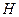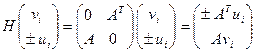. (5)

Рассмотрим составляющие правой части (5):

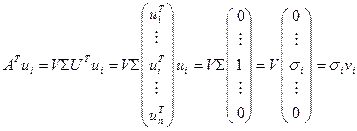. (6)

Аналогично (6) показывается, что

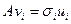. (7)

Учитывая (6) и (7), из (5) вытекает

,

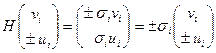из чего по определению следует, что 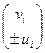— СВ матрицы 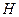, отвечающий СЗ 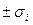, который после нормирования становится равным .

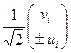Опираясь на установленную связь между сингулярным и спектральным разложениями соответствующих матриц, можно преобразовать алгоритмы решения симметричной проблемы СЗ в алгоритмы вычисления сингулярного разложения. Это преобразование выполняется не прямолинейно, поскольку сингулярное разложение обладает дополнительной структурой, которая часто может быть использована для повышения эффективности и точности алгоритмов.