Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Два представления о сходимости QR-, QL-алгоритмов

Рассмотрим вопрос о сходимости 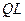-алгоритма. Если сдвиги 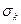не используются, то 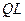-алгоритм называется основным.

Вообще с 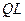, 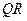-алгоритмами связаны два представления о сходимости. Строго говоря, сходимость 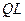, 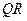-алгоритмов нужно понимать как сходимость матричной последовательности 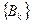. В общем случае можно показать, что такая последовательность сходится к диагональной матрице, на диагонали которой находятся собственные значения исходной матрицы 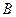(симметричной). Если 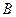- несимметричная матрица, то матричная последовательность 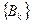сходится к блочно-диагональной матрице, каждый диагональный блок которой отвечает собственному значению.

Однако можно понимать сходимость несколько иначе.

Теорема (случай симметричной матрицы). Пусть собственные значения матрицы 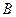удовлетворяют условию:

.

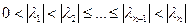Пусть матричная последовательность 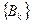получена основным 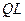-алгоритмом, тогда имеет место равенство:

,

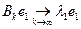где .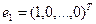

В соответствии с приведенной теоремой сходимость понимается как стремление к 0 внедиагональных элементов первого столбца матрицы. На практике как только 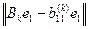становится малой, это означает, что элемент 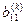можно рассматривать как приближенное значение собственного значения 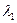. После этого, если 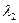не является кратным, итерационный процесс можно продолжить для матрицы размера 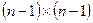, отбросив первую строку и первый столбец, и т.д.