
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сохранение ширины ленты матрицы в QR-, QL-алгоритмах
|
|
Лекция 26. Алгоритмы решения полной проблемы собственных значений
План
QR-, QL-алгоритмы решения полной проблемы собственных значений
Два представления о сходимости QR-, QL-алгоритмов
Ускорение сходимости QR-, QL-алгоритмов. Сдвиг по отношению Рэллея, по Уилкинсону.
Сохранение ширины ленты матрицы в QR-, QL-алгоритмах
- QR-, QL-алгоритмы решения полной проблемы собственных значений
QR-, QL-алгоритмы решения полной проблемы собственных значений наиболее эффективны для небольших матриц (размера 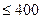 ). Эти алгоритмы эффективны для симметричных ленточных матриц, особенно для трехдиагональных.
). Эти алгоритмы эффективны для симметричных ленточных матриц, особенно для трехдиагональных.
Основная идея: QR-, QL-алгоритмы за счет подобных преобразований быстро уменьшают внедиагональные элементы, пока они не станут пренебрежимо малыми.
Любая ненулевая матрица 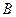 може быть представлена в виде произведения:
може быть представлена в виде произведения:
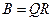 (1)
(1)
где 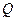 - ортогональная вещественная матрица (т.е.
- ортогональная вещественная матрица (т.е. 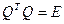 ,
, 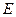 - единичная матрица соответствующего размера),
- единичная матрица соответствующего размера), 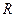 - верхняя треугольная матрица с неотрицательными диагональными элементами. Матрицы
- верхняя треугольная матрица с неотрицательными диагональными элементами. Матрицы 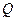 и
и 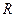 определяются однозначно.
определяются однозначно.
Если 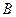 - невырожденная вещественная матрица, то
- невырожденная вещественная матрица, то 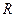 - это верхний множитель Холесского для симметричной положительно определенной матрицы
- это верхний множитель Холесского для симметричной положительно определенной матрицы 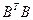 :
:
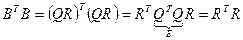 .
.
Для матрицы 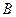 возможно разложения вида:
возможно разложения вида:
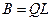 (2)
(2)
где 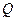 - ортогональная вещественная матрица (т.е.
- ортогональная вещественная матрица (т.е. 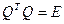 ,
, 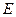 - единичная матрица соответствующего размера),
- единичная матрица соответствующего размера), 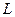 - нижняя треугольная матрица. Эта матрица получается из соответствующего разложения матрицы
- нижняя треугольная матрица. Эта матрица получается из соответствующего разложения матрицы 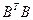 с учетом
с учетом 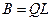 :
:
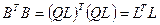 .
.
Пример. Построить 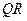 ,
, 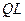 - разложения матрицы
- разложения матрицы
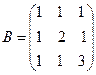 .
.
Матрица 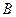 является невырожденной, поэтому
является невырожденной, поэтому 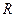 - верхний множитель Холесского для матрицы
- верхний множитель Холесского для матрицы 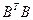 . Вычислим элементы матрицы
. Вычислим элементы матрицы 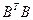 и построим для нее разложение Холесского:
и построим для нее разложение Холесского:
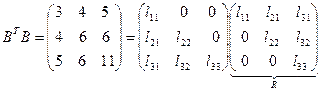 ,
,
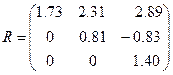 .
.
Элементы матрицы 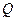 определяются из матричного соотношения:
определяются из матричного соотношения:
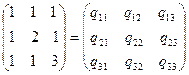
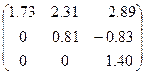 ,
,
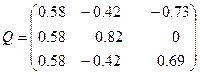 .
.
Таким образом, 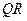 - разложение исходной матрицы выглядит следующим образом:
- разложение исходной матрицы выглядит следующим образом:
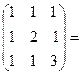
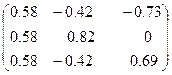
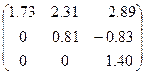 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Построим теперь для матрицы 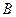
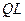 - разложение. Для этого:
- разложение. Для этого:
 .
.
Составляя уравнения для элементов матрицы 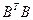 в порядке, отмеченном выше, получим
в порядке, отмеченном выше, получим
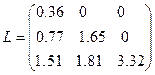 .
.
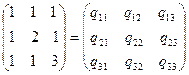
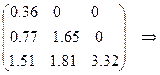
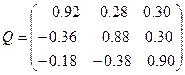 .
.
Таким образом, 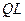 - разложение исходной матрицы выглядит следующим образом:
- разложение исходной матрицы выглядит следующим образом:
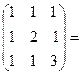
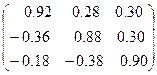
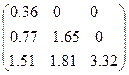 .
.
Для определенности рассмотрим далее 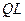 -алгоритм.
-алгоритм.
Пусть дана матрица 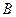 и число
и число 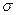 , называемое сдвигом (сдвиг используется для ускорения сходимости
, называемое сдвигом (сдвиг используется для ускорения сходимости 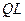 -алгоритма). Для матрицы
-алгоритма). Для матрицы 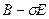 построим
построим 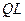 -разложение:
-разложение:
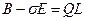 . (3)
. (3)
Из (3) выразим 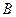 :
:
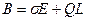 . (4)
. (4)
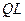 -преобразование матрицы
-преобразование матрицы 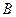 с учетом (4) определим следующим образом:
с учетом (4) определим следующим образом:
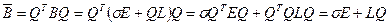 . (5)
. (5)
Поскольку 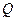 - ортогональная матрица, это преобразование является подобным.
- ортогональная матрица, это преобразование является подобным.
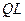 -алгоритм.
-алгоритм.
Обозначим исходную матрицу 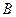 через
через 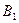 . Для
. Для 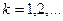 делать
делать
1. Определить сдвиг 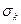 , построить
, построить 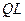 -разложение матрицы
-разложение матрицы 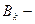
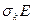 :
:
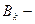
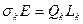 .
.
2. Построить 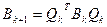 .
.
3. Проверка сходимости алгоритма.
Числа 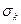 выбираются так, чтобы ускорить сходимость
выбираются так, чтобы ускорить сходимость 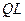 -алгоритма. Каждый шаг алгоритма генерирует очередную матрицу
-алгоритма. Каждый шаг алгоритма генерирует очередную матрицу 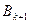 , подобную исходной матрице
, подобную исходной матрице 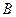 .
.
|
|
