
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Незатухающие гармонические колебания
|
|
Гармонические колебания совершаются под действием упругих или квазиупругих (подобные упругим) сил, описываемых законом Гука:
 ,
,
где F – сила упругости;
х –смещение;
k – коэффициент упругости или жесткости.
Согласно ІІ закону Ньютона 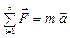 , где а – ускорение, а =
, где а – ускорение, а = 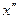 .
.
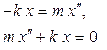
| (1) |
Разделим уравнение (1) на массу m и введем обозначение 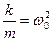 , получим уравнение в виде:
, получим уравнение в виде:
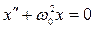 (2).
(2).
Уравнение (2) – дифференциальное уравнение незатухающих гармонических колебаний.
Его решение имеет вид: 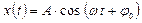 или
или 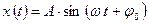 .
.
Характеристики незатухающих гармонических колебаний:
х – смещение; А – амплитуда; Т – период; 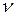 – частота;
– частота; 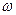 – циклическая частота,
– циклическая частота, 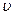 – скорость;
– скорость; 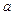 – ускорение,
– ускорение,  – фаза;
– фаза;  0 – начальная фаза, Е – полная энергия.
0 – начальная фаза, Е – полная энергия.
Формулы:
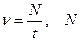 – число колебаний, – число колебаний, 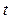 – время, за которое совершается N колебаний; – время, за которое совершается N колебаний;
|
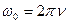 , , 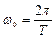 ; ; 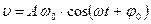 или или 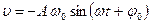 ; ;
|
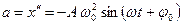 или или 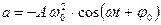 ; ;
|
 – фаза незатухающих гармонических колебаний; – фаза незатухающих гармонических колебаний;
|
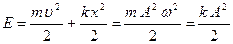 – полная энергия гармонических колебаний. – полная энергия гармонических колебаний.
|
|
|
