Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Формула (закон) Пуазейля

Основной движущей силой является кровяное давление, обусловленное превышением давления, вызванного работой сердца, над атмосферным.

,

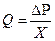где 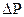– разность давлений на входе и выходе сосуда;

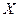– гидравлическое сопротивление сосуда;

,

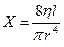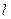– длина сосуда, 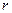– внутренний радиус сосуда,

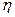– динамический коэффициент вязкости жидкости.

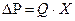
Давление крови в сосудах зависит от объемной скорости кровотока, радиуса сосуда, вязкости крови.

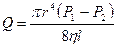
Согласно формуле объемная скорость кровотока пропорциональна градиенту давления: 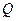~ 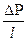(градиент давления) и обратно пропорциональна вязкости.

Однако может показаться удивительным, что 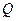~ 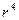(радиус в четвертой степени). Это означает, что при одном и том же градиенте давления увеличение радиуса вдвое приводит к увеличению объемной скорости кровотока в 16 раз!

Интересный пример зависимости 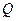~ 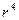можно найти и в системе кровообращения человеческого организма.

Поскольку формула Пуазейля справедлива лишь для ламинарного течения несжимаемой жидкости с постоянной вязкостью, то она не может в точности выполнятся для крови. Так как кровь содержит взвешенные частицы, то течение крови не вполне ламинарно, а ее вязкость зависит от скорости течения. В этом случае формула Пуазейля является хорошим приближением в первом порядке. Однако, при атеросклерозе и отложении холестерина радиус сосудов уменьшается и тогда для поддержания нормального кровотока требуется более высокий градиент давления.