Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Таблично задана лінія регресії

k	xk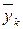
	53, 95 102, 27 169, 40	239, 93 342, 84 434, 10

Для наочності побудуємо графік лінії регресії. Для цього в прямокутній системі координат 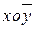зобразимо точки з координатами (x_k; 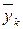) (тобто кореляційне поле) і послідовно сполучимо їх відрізками прямих (див. рис.3.7).

Із аналізу таблиці 3.6 і графіка (рис. 3.7) можна зробити такий висновок: більшим витратам на утримання відповідають більші перерахування до бюджету, що підтверджує попередній висновок про можливість існування прямого зв’язку між Х та Y, зроблений за результатами комбінаційного групування. При цьому із вигляду графіка можна припустити, що зростання Y має, можливо, сповільнений характер.

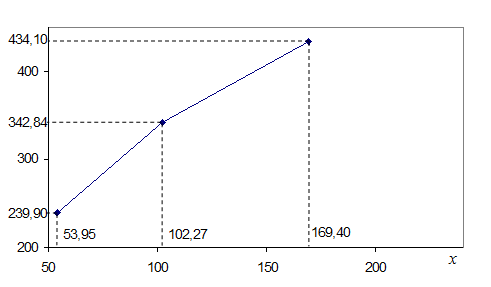
Рис. 3.7. Графік таблично заданої лінії регресії

3. Метод дисперсійного аналізу (п. 2.3)

Усю сукупність 20-ти пар (х_і; у_і), що вивчається, розділимо за факторною ознакою на 3 групи, використавши поділ, зроблений у таблиці 3.5. За формулою (3.1) обчислимо загальну середню 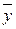для всієї сукупності значень у_і (і = ):

.

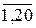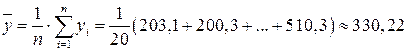За формулою (3.3) обчислимо загальну дисперсію ознаки Y:

.

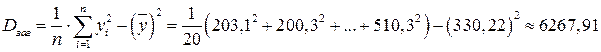За формулою (3.6) обчислимо міжгрупову дисперсію, використавши раніше знайдені значення групових середніх 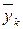(табл. 3.6) і частот f_k (табл. 3.4):

.

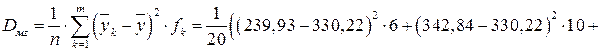
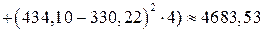За формулою (3.8) обчислюємо спостережене значення кореляційного відношення:

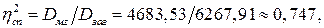
звідки витікає, що 74, 7 % загальної варіації ознаки Y пов’язано з варіацією ознаки Х, а це свідчить про можливість існування залежності Y від Х.

Для формального підтвердження або спростування даного припущення знайдемо критичне значення величини η ² для рівня значущості 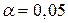. За таблицею критичних значень (додаток 2) для степенів вільності k ₁ =m– 1=3–1=2, k ₂ =n–m =20–3=17 знаходимо 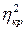= =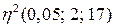0, 297. Оскільки 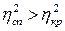, то з імовірністю 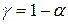=0, 95 можна вважати, що Y істотно залежить від Х. Для оцінки щільності зв’язку застосовуємо правило трисекції: 0, 7 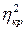+ 0, 3=0, 508; 0, 3 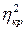+ 0, 7=0, 789. Оскільки 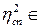[0, 7 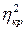+ 0, 3; 0, 3 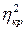+ 0, 7], то щільність зв’язку будемо вважати помірною.