Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Теорема о трех непараллельных силах.

Если твердое тело под действием трех непараллельных сил, две из которых пересекаются, находится в равновесии, то ли­нии их действия пересекаются в одной точке.

Задача 1. На середину балки АВ действует сила 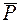(рис. 16). В точке А балка имеет шарнирно-неподвижную опору, а в точке В — шарнирно-подвижную. Определить линию действия реакции в точ­ке А.

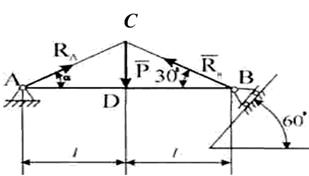
Рис. 16

Решение. Реакция 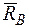шарнирно-неподвижной опоры пер­пендикулярна опорной поверх­ности и пересекается с линией действия силы Р в точке С. По теореме о трех непараллельных силах реакция опоры А должна пройти через эту точку:

.

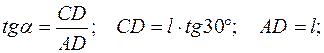
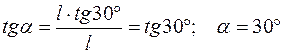Ответ. Реакция 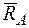образует- угол 30° с осью балки АВ.

Задача 2. Два невесомых стержня, соединенные в точке С шарниром, удерживают груз Р = 50 Н, который нитью прикреплен к шарни­ру С. Найти усилия в стержнях АС и ВС, если 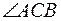= 60°.

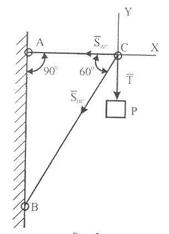
Рис.17

Решение. Используя принцип освобождаемости от связей, заменяем действие стержней АС, ВС. и нити на шарнир С реакциями 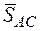, , 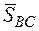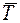. Учтем, что Т= Р = 50 Н Реакции показаны на рис. 17. Считаем стерж­ни растянутыми и не делаем допол­нительный рисунок. Запишем урав­нения равновесия, учитывая, что конструкция находится в плоскости СХУ. Направления осей показаны на рисунке.

1.

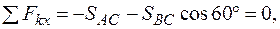
2. .

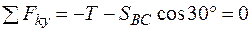Находим из (2)

,

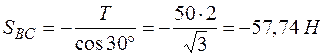из (1)

.

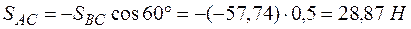Отрицательное значение указывает, что стержень ВС сжат, а не растянут, как предполагалось.

Задача 3. Груз весом G = 2 кН (рис. 1) удерживается краном, состоящим из двух невесомых стержней в шарнирах АВ и АС, прикрепленных к вертикальной стене и составляю­щих с ней углы α ₁ = 60° и α ₂ = 40°. В точке А подвешен блок, через который перекинут грузовой трос, идущий к блоку в точке D и составляющий со стеной угол α ₃ = 60°.

Весом троса и блока, а также размерами блока можно пренебречь. Определить усилия в стержнях.

Решение. Рассмотрим находящийся в равновесии груз (рис. 2).

На него действуют две силы: сила тяжести G и сила натяжения троса N ₁. Поскольку система сил уравнове­шена, можно сделать очевидный вывод: сила натяжения троса направлена внутрь троса и по модулю равна весу груза N ₁ = G.

Если для любого блока (рис. 3) пренебречь трением на его оси, то силы натяжения ветвей его троса одинаковы N ₁ = N ₂ (что легко видеть из уравнения моментов относи­тельно центра блока).

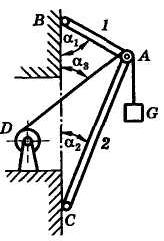
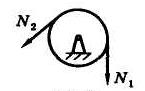
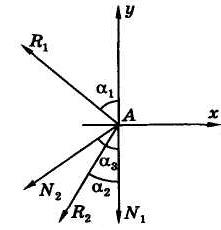
Рис. 1 Рис. 2 Рис. 3 Рис. 4

Теперь в качестве объекта равновесия можно рассмот­реть мысленно вырезанный узел в точке А (или, что то же самое, блок с прилежащей к нему частью троса). На этот узел будут действовать силы натяжения ветвей троса N ₁ и N ₂ и реакции R ₁ и R ₂ стержней АВ и АС (рис. 4).

Реакции опорных стержней направлены, как извест­но, вдоль этих стержней. Направим их внутрь стержней, считая изначально стержни растянутыми.

Составим теперь уравнения равновесия как уравне­ния проекций сил на оси (для системы сходящихся сил), учитывая, что силы R ₁, R ₂ и N ₂ составляют углы α ₁, α ₂ и α ₃ с осью у.

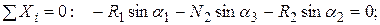
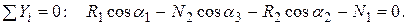
Отсюда, учитывая, что 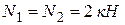, получаем

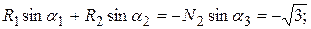
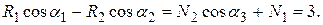
Решая эту систему уравнений, находим R ₁ = 0, 611 кН, R ₂ = –3, 52 кН. Знак «минус» у величины реакции R ₂ озна­чает, что она имеет направление, противоположное при­нятому, то есть стержень АС не растянут, а сжат.

Ответ: R ₁ = 0, 611 кН, R ₂ = –3, 52 кН.

Задача 4. На невесомую балку, закрепленную с помощью не­подвижного шарнира в точке А и троса в точке В, действу­ет сила F, модуль которой F = 5 кН (рис. 5). Учитывая указанные на рисунке геометриче­ские размеры, определить реакции опор балки.

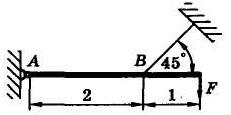
Рис. 5

Решение. Рассмотрим балку, воспользуемся принципом освобож­даемости от связей, отбросим их и введем соответствующие реакции. Реакция троса в точке В, как известно, направлена по тросу, а реакция шарнирно-неподвижной опоры имеет не­известное направление.

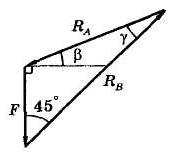
Рис. 6 Рис. 7

Однако в данном случае определить ее направление позволяет теорема о трех силах, согласно которой линии действия трех непараллельных сил, под действием кото­рых тело находится в равновесии, должны пересекаться в одной точке. В рассматриваемой схеме это будет точка О пересечения линий действия силы F и линии троса (рис. 6).

Таким образом, реакция в точке А проходит по линии АО под углом β, величину которого найдем из треугольни­ка: tg β = 1/3 и β = arctg 1/3.

Для определения величин реакций могут быть приме­нены три способа: графический, графоаналитический и аналитический.

1. Графический способ. Следует построить в масштабе замкнутый силовой многоугольник, начиная с известной силы F, а затем в произвольной последовательности ос­тальные силы R_A и R_B.

Например, можно провести из конца силы F линию действия реакции R_B, а из ее начала — линию действия R_A до их пересечения. Силы должны быть направлены в одну сторону по пути обхода контура (рис. 7).

Затем, измеряя отрезки и сравнивая их с масштабом, можно узнать величины неизвестных сил.

2. Графоаналитический способ. Здесь также строится силовой многоугольник, но только в виде геометрической схемы, рассматривая которую можно вычислить неизвестные стороны треугольника.

Для схемы (рис. 7) согласно теореме синусов получаем

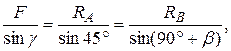
где γ = 180°– 45° – (90° + β) = 45°– β.

Из этих уравнений имеем

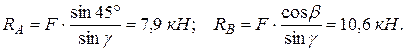
3. Аналитический способ. Здесь не требуется построе­ния силового многоугольника, необходима лишь расчет­ная схема с направлениями реакций (рис. 8). При этом не по линии действия направлять не­известные силы.

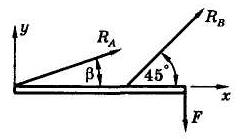
Рис. 8

Выбирая координатные оси х и у, записываем уравнения рав­новесия в проекциях на эти оси:

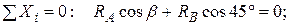
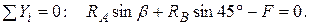
Решая эту систему уравнений, получаем

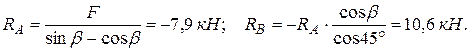
Отрицательный знак у величины R_A означает, что дей­ствительное направление этой реакции противоположно выбранному на схеме.

Ответ: R_A = –7, 9 кН; R_B = 10, 6 кН.

Задача 5. Подвеска идеального блока О лебедки состоит из трех невесомых стержней в шарнирах: двух горизонтальных АО и ВО, составляющих углы 45° с перпендикуляром к стене DO, и стержня СО, составляющего угол 60° с вертикальной линией стены DE (рис. 9).

Через блок перекинут трос, на од­ном конце которого подвешен непо­движный груз весом G = 10 кН. Дру­гой конец, уходящий на лебедку, в точке Е стены составляет угол 30° с вертикалью DE. Определить усилия в стержнях подвески.

Решение. В качестве объекта, равновесие которого следует рассмот­реть, выберем блок вместе с прилега­ющей к нему частью троса (узел в точке О).

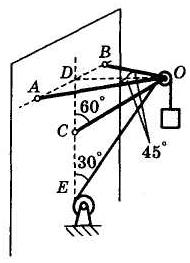
Рис. 9

При условии, что размерами его можно пренебречь, действующие на него силы представляют собой си­стему сходящихся сил. Учитывая, что реакции опорных стержней на­правлены по линиям этих стержней, а силы натяжения — по тросу, полу­чаем расчетную схему (рис. 10).

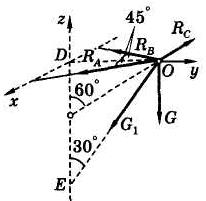
Рис. 10

Здесь G ₁ = G — сила натяжения ветви троса, идущей к лебедке в точке Е; направления реакций стержней выбраны в предпо­ложении, что стержни АО и ВО растянуты, а стержень СО — сжат.

Для удобства геометрического рассмотрения начало координат взято в точке D, ось х направлена по линии АВ, ось у — по DO, ось z — по DE.

Записываем теперь условие уравновешенности систе­мы сходящихся сил.

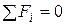в проекциях на декартовы оси:

х: R_A sin 45° – R_B sin 45° = 0;

у: – R_A cos 45° – R_B cos 45° + R_С sin 60° – G sin 30° = 0;

z: R_С cos60^о – G ₁cos30° – G = 0.

Решая эту систему, находим значения усилий в стерж­нях подвески:

R_С = 37, 3 кН; R_A = R_B = 19, 3 кН.

Все усилия получились положительными, значит их направления были изначально взяты правильно.

Можно отметить при этом, что усилия в стержнях под­вески оказались значительно большими, чем вес удержи­ваемого ими груза, и существенно зависят от геометриче­ских параметров (углов) самой конструкции подвески.

Ответ: R_С = 37, 3 кН; R_A = R_B = 19, 3 кН.

Базовые вопросы

1.Сущность аксиом статики.

2.Cущность принципа освобождаемости от связей.

3.Виды связей и их реакции.

4. Дайте определение системы сходящихся сил.

5. Как найти равнодействующую системы сходящихся сил гра­фическим методом?

6. Как определить равнодействующую системы сходящихся сил аналитическим методом?

7. Сформулируйте условия равновесия системы сходящихся сил.

8. Сущность теоремы о трех непараллельных силах.