Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

В цилиндрических трубопроводах

7.1. Основные зависимости для гидравлического расчёта трубопроводов

Преобразуем формулу потерь напора по длине 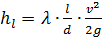при турбулентном режиме движения жидкости, учтя, что d=4R:

,

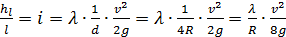откуда

.

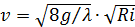Обозначим

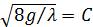. (7.1)

Тогда

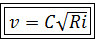(7.2)

или

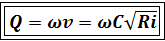. (7.3)

Формулы (7.2) и (7.3) носят имя А. Шези. Их применяют для расчёта средней скорости и расхода потока в каналах, реках и безнапорных трубах. Коэффициент C при квадратичной области сопротивлений определяют по эмпирическим и полуэмпирическим формулам, например, по формуле Н. Н. Павловского

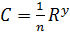, (7.4)

где n – коэффициент шероховатости русла, зависящий от материала стенок и их состояния; R – гидравлический радиус, м; y – показатель степени, зависящий от R и n. Павловский считал формулу (7.4) пригодной при 0, 1≤ R≤ 3, 0 м и 0, 011≤ n≤ 0, 040.

Из формулы Шези вытекают зависимости, широко применяемые при расчётах как напорных, так и безнапорных трубопроводов и открытых русл. Разделив (7.2) и (7.3) на 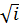, получим соответственно

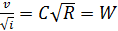; (7.5)

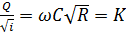; (7.6)

откуда следует, что

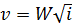; (7.7)

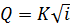. (7.8)

Здесь W – модуль скорости (скоростная характеристика); K – модуль расхода (расходная характеристика).

Разрешив (7.2) и (7.3) относительно уклона i, получим

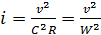; (7.9)

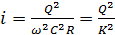. (7.10)

Умножив (7.9) и (7.10) на l, найдём:

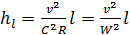; (7.11)

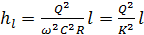. (7.12)

Обозначив 1/ K ²= A, получим

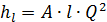, (7.13)

,

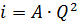где величина A=1/ K², равная потере напора на единицу длины трубопровода при единичном расходе, носит название удельного сопротивления трубопровода.

Формулу (7.13) можно записать в виде

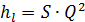, (7.14)

где S - сопротивление трубопровода.

Величины K, A, S – обобщённые гидравлические параметры трубопровода, использование которых значительно ускоряет расчёт.

Зависимости (7.8), (7.12), (7.13) и (7.14) - основные расчётные формулы простого трубопровода при равномерном движении жидкости.

Если область сопротивления отличается от квадратичной, значение расходной характеристики K определяется по формуле

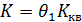, (7.15)

где

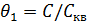. (7.16)

Значения коэффициента θ ₁≤ 1 получены Ф. А. Шевелёвым для основных видов водопроводных труб и приводятся в справочной литературе.

С учётом (7.15) расчётные зависимости (7.8) и (7.12) примут вид

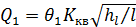, (7.17)

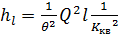. (7.18)

Формулу (7.18) можно также представить в виде

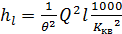. (7.19)

где l – длина трубопровода в км, а значения 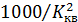приводятся в справочной литературе.