Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение реакций в кинематических парах.
|
|
Определение давлений в кинематических парах начинаем с рассмотрения равновесия группы Ассура (2-3) (Рисунок 3): шатун AB – ползун B. На звенья этой группы действуют силы: движущая сила Fд, силы тяжести G 3, G 2, результирующие силы инерции Ф3, Ф2, реакция R 03 заменяющая действие стойки 0 на ползун 3 и реакция R 12 заменяющая действие кривошипа 1 на шатун 2.
Силы, приложенные в точке B, приводим к одной силе F 3.Величину этой силы определяем по формуле:
F3=-Ф3-G3+Fд (40)
F3=-821.1918-7.6528+43000=42171.156 Н
Знак (+) показывает, что сила F 3 направлена вверх.
Условие равновесия группы (2-3) выражается следующим образом:
+ 
+ 
+ 
+ 
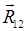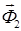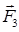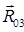=0 (41)
Давление R 12 раскладываем на две составляющие, действующие вдоль оси звена AB – R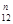 
и перпендикулярно к оси звена AB – R 
.
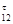Составляющую R 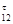определяем из уравнения моментов всех сил, действующих на шатун AB, относительно точки B.
Применительно к рисунку 3 это уравнение можно записать так:
R 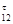*l2-Ф2× h1-G2× h2=0 (42)
откуда
R 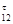=(Ф2× h1+G2× h2)/l2 (43)
R 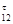= (5365.72× 231+25.506× 42)/300=4135.175Н.
План сил строим в масштабе: mF =421.71156 Н/мм.
Из произвольной точки последовательно откладываем вектора R 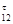, F 3+ G 2, Ф2. Через конечную точку вектора Ф2 проводим линию действия реакции R 03, а через начальную точку вектора R 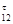-линию действия силы R 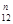. Получим точку пересечения. Соединив конечную точку вектора Ф2 с точкой пересечения, получим вектор R 03. Соединив точку пересечения с конечной точкой вектора R 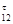, получим вектор R 12.Умножив соответствующие длины на масштабный коэффициент, получим: R 03 = 8499.8 H; R 12 = 40858.6 H; R 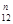= 4135.2 Н
Если из произвольной точки отложить вектор R 12 для всех двенадцати положений, то получим годограф реакции R 12.
По результатам расчета программы ТММ1 строим годограф реакции R 12 в масштабе mR =618.4858 Н/мм.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Если в каждом из двенадцати положений ползуна отложить вектор R 03 и соединить их конечные точки плавной кривой, то получим годограф реакции R 03.
По результатам расчета программы ТММ1 строим годограф реакции R 03= R 03(SB) в масштабе mR =170.04Н/мм
Давление R 32 в паре шатун – ползун определяем из условия равновесия ползуна:
+ 
+ 
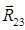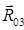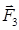=0 (44)
и равенства:
R32=R23, (45)
или
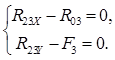(46)
Тогда
R23X=R03=8502.36 H,
R23Y=F3=42171.15 H;
R23=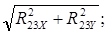 
(47)
R23=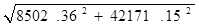 
=43022.68 Н
R32=43022.68 Н
По результатам расчета программы ТММ1 строим диаграмму реакции R 32= R 32(j 1) в масштабе: mR =1146.004 Н/мм.
3.3 Силовой расчёт механизма I класса.
К кривошипу приложена сила тяжести G 1, известная реакция R 21=- R 12. Неизвестная по значению и направлению реакция R 01 показана в виде R 
и R 
.
Чтобы кривошип мог совершать вращение по заданному закону, к нему со стороны отсоединённой части машинного агрегата должна быть приложена реактивная нагрузка в виде уравновешивающей силы Fy. Допустим, что неизвестная по модулю уравновешивающая сила приложена перпендикулярно кривошипу в точке А.
Силу инерции кривошипа не определяем, так как он уравновешен.
|
|