Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Вопрос 16. Энергетический спектр случайных сигналов

Одним из эффективных средств анализа сигналов является частотный метод, основанный на представлении сигналов при помощи преобразования Фурье, а цепи – в виде частотной передаточной характеристики. Естественным является использовать математический аппарат частотного метода для анализа случайных процессов. Но случайный процесс, представляющий собой множество (ансамбль) детерминированных реализаций, не может быть описан комплексной спектральной плотностью, даже и усредненной, так как из-за случайности и независимости фаз составляющих в различных реализациях усреднение приводит к нулевому результату (при mx =0). Однако можно ввести понятие спектральной плотности среднего квадрата случайного сигнала, поскольку средний квадрат не зависит от соотношения фаз суммируемых гармоник. Если под случайной функцией x(t) подразумевается электрическое напряжение или ток, то её средний квадрат можно

рассматривать как среднюю мощность, выделяемую в сопротивлении 1 Ом. Эта мощность распределена по частотам в некоторой полосе частот, зависящей от механизма образования случайного процесса. Спектральная плотность средней мощности представляет собой среднюю мощность, приходящуюся на 1 Гц при заданной частоте. Её размерность определяется отношением мощности к полосе частот, т. е. является размерностью энергии.

Для определения спектральной плотности случайного сигнала выделим из ансамбля одну реализацию xk(t) длительностью Т. Для неё как для детерминированной функции может быть определена спектральная плотность:

T/2

X_K ^T (w)=ò x_k (t) e^{-jσ x}dt

-T/2

Полная энергия рассматриваемого отрезка k -й реализации равна

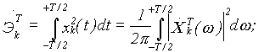
отсюда получаем среднюю мощность

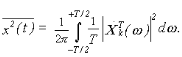
При увеличении интервала Т энергия отрезка возрастает, однако средняя мощность (из-за 1/T) стремится к некоторому пределу

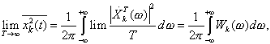
где Wk(w) представляет собой спектральную плотность мощности k -й реализации. Спектральная плотность процесса Wx(w) получается усреднением по всем реализациям.

Если процесс стационарный и эргодический, то Wk(w) характеризует весь процесс в целом, и усреднения не требуется, то есть Wх (w) = Wk(w). Если случайный процесс имеет ненулевое математическое ожидание, то спектральную плотность следует представлять в форме

Wx(w)=m_x ²2π δ (w)+W*(w)

где W*(w) – cплошная часть спектра, соответствующая флуктуационной составляющей.

При интегрировании по частоте f=w /2π первое слагаемое дает величину m_x², то есть мощность постоянной составляющей, а второе – мощность флуктуаций, то есть дисперсию

+∞

D_x=σ _x ² = ò W^*_x (w)dw

-∞

Поскольку спектральная плотность мощности случайного процесса определяется как модуль квадрата спектральной плотности реализации, то функция Wx(w) является неотрицательной и четной.