Вопрос 5. Спец.функции: дельта-функции. Их свойства. Пример использования

Спектральная плотность дельта-функции общего вида s(t)=δ (t – t0), выставленную в точке временной плоскости t0, определим с помощью прямого преобразования Фурье (1.10):

¥

S(jw) = ò δ ( t – t0 ) exp(-jwt) dt = exp(-jwt0),

-¥

а для дельта-функции расположенной в начале координат получим:

¥

S(jw) = ò d(t) exp(-jwt) dt = 1.

-¥

Графики характеризующие дельта-функцию во временной и спектральной областях приведены на рис. 1. Из рисунка следует, что дельта-функция имеет равномерный (сплошной и бесконечный) спектр с единичной интенсивностью на всех частотах. Т. к. в спектральной области модуль спектральной плотности дельта-функции не ограничен по протяженности, это позволяет использовать функцию как испытательную при нахождении временных характеристик линейных цепей – импульсной характеристики.

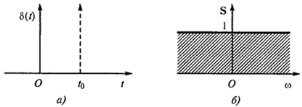
Рис. 1. Дельта-функция во временной области (а)

и её модуль спектральной плотности (б)

При таких исследованиях достаточно воздействия не идеальной модели рассматриваемой функции, а просто очень коротких импульсов напряжения на линейные цепи. При этом не обязательно, чтобы длительность реального импульса была бесконечно мала, а амплитуда бесконечно велика. Оказывается достаточным условием является, чтобы длительность импульса была много меньше периода собственных колебаний линейной цепи.

Для дельта-функции можно найти обратное преобразование Фурье в виде:

¥

d(t) = (1/2p) ò exp(jwt) dw,

-¥

которое широко используется при различных вычислениях. Физически представить свойства и параметры дельта-функции достаточно просто. Так, в момент возникновения импульса (t = 0) все элементарные гармонические составляющие бесконечного спектра дельта-функции

суммируются когерентно (синфазно), поскольку в соответствии с полученными выражениями спектральная плотность дельта-функции вещественна. Поэтому при t = 0 наблюдается бесконечно большая амплитуда импульса.

· Спектральная плотность гармонического сигнала. Определим спектральную плотность гармонического (положим, что косинусоидального) сигнала единичной амплитуды s(t)=cos ω 0 t, для которого условия применимости преобразования Фурье не выполняются. Подставив в прямое преобразование Фурье (1.10) заданный сигнал, и воспользовавшись формулой Эйле

ра e^jx =cos x + j sin x, а, также выполнив необходимые преобразования, получим:

¥

S(jw) = ò cos ω 0 t exp(-jwt) dt = π [δ (ω - ω 0) + δ (ω + ω 0)],

-¥

следовательно, спектральную плотность гармонического сигнала можно отобразить двумя дельта-функциями в частотной области, с координатами – - ω 0 и + ω 0.

По аналогии с косинусоидальным сигналом нетрудно показать, что синусоидальному сигналу s(t)=sinω 0 t отвечает спектральная плотность S(jw)=π [δ (ω - ω 0) - δ (ω + ω 0)]. Здесь знак минус появляется вследствие нечетности функции синусоидального сигнала.

Дельта-функция обладает фильтрующим свойством. Суть его заключается в том, что если дельта-функция d(t-t) входит под интеграл какой-либо функции в качестве множителя, то результат интегрирования равен значению подынтегральной функции в точке t расположения дельта-функции, т. е.:

¥

ò s(t) d(t-t) dt=s(t).

- ¥

Пределы интегрирования в этом выражении можно ограничить ближайшими окрестностями точки t.

Спектральная плотность постоянного напряжения (тока). Спектральную характеристику постоянного напряжения, например, единичной амплитуды можно легко определить, приравняв в формулах для спектральной плотности рассмотренных гармонических сигналов частоту ω 0 к нулевому значению. В результате получим: S(jw)=2π δ (ω), т. е. это дельта-функция в начале координат частотной области. Физический смысл данного результата

достаточно прост и очевиден, т. к. постоянный во времени сигнал может иметь единственную спектральную составляющую в отмеченной области. Подобные расчеты можно продолжить и для других сигналов, но эти исследования являются предметом практических занятий с использованием известных программ.