
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Корреляционный анализ
|
|
При научных исследованиях чаще всего имеют дело со связями, при которых определенному значению одной переменной соответствует некоторый размах второй. Такие виды зависимостей называют корреляцией. Сила взаимосвязи выражается степенью концентрации точек вокруг линии регрессии. Показателем силы связи является для прямолинейной зависимости коэффициент корреляции r, а для криволинейной – корреляционное отношение  .
.
Тесноту связи по r иможно оценить по придержкам, предложенным М.Л. Дворецким (1971): до 0, 30 – слабая, 0, 31-0, 50 – умеренная, 0, 51-0, 70 – значительная, 0, 71-0, 90 – высокая, 0, 91 и более – очень высокая.
Коэффициент корреляции вычисляется несколькими способами. Далее приводится табл. 4.9 и пример его вычисления для малой выборки между диаметром ствола на высоте 1, 3 м и диаметром кроны дерева.
Таблица 4.9
Таблица для вычисления коэффициента корреляции
между диаметром ствола и диаметром кроны
| Д1, 3, см (хi) | Д кр., м (yi) | хi-Мх
( ) )
| yi-Мy
(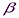 ) )
| 2 | 2 | |
| 2, 1 | -7 | -1, 4 | 9, 8 | 1, 96 | ||
| 3, 0 | -2 | -0, 5 | 1, 0 | 0, 25 | ||
| 1, 3 | -11 | -2, 2 | 24, 2 | 4, 84 | ||
| 5, 1 | 1, 6 | 11, 2 | 2, 56 | |||
| 6, 5 | 3, 0 | 42, 0 | 9, 00 | |||
| 3, 0 | -1 | -0, 5 | 0, 5 | 0, 25 | ||
| ∑: 114 | 21, 0 | 88, 7 | 18, 86 |
Мx =  =
=  = 19 (cм); Мy =
= 19 (cм); Мy =  =
= 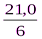 = 3, 5 (м);
= 3, 5 (м);
r =  =
= 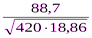 =
=  = 0, 99;
= 0, 99;
mr = ± 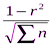 =±
=±  = ± 0, 008; r = 0, 99 ± 0, 008.
= ± 0, 008; r = 0, 99 ± 0, 008.
Таким образом, теснота связи между диаметром ствола и диаметром кроны дерева оказалась очень высокой.
Корреляционное отношение вычисляется, когда зависимость между двумя переменными передается через уравнение кривой. Далее приводится табл. 4.10 и пример вычислениямежду диаметром деревьев на высоте 1, 3 м и их высотой (при малой выборке).
= 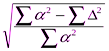 =
= 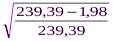 =
= 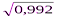 = 0, 996;
= 0, 996;
m  = ±
= ±  = ±
= ±  = ± 0, 002;
= ± 0, 002;
= 0, 996 ± 0, 002.
Таблица 4.10
Таблица для вычисления корреляционного отношения между диаметром стволов и их высотой
| Диаметр, см | Высота, м (h) | Высота ступени толщины, см (hст) | Н-h () | 2 |  =h-hст =h-hст
| 2 |
| 14, 3 14, 9 15, 1 | 15, 1 | 6, 1 5, 5 5, 3 | 37, 21 30, 25 28, 09 | -0, 8 -0, 2 | 0, 64 0, 04 | |
| 16, 5 16, 1 | 16, 3 | 3, 9 4, 3 | 15, 21 18, 49 | 0, 2 -0, 2 | 0, 04 0, 04 | |
| 18, 4 | 18, 4 | 2, 0 | 4, 00 | |||
| 19, 5 21, 0 20, 1 | 20, 2 | 0, 9 -0, 6 0, 3 | 0, 81 0, 36 0, 09 | -0, 7 0, 8 -0, 1 | 0, 49 0, 64 0, 01 | |
| 21, 2 21, 4 | 21, 3 | -0, 9 -1, 0 | 0, 81 1, 00 | -0, 1 0, 1 | 0, 01 0, 01 | |
| 22, 5 22, 7 | 22, 6 | -2, 1 -2, 3 | 4, 41 5, 29 | -0, 1 0, 1 | 0, 01 0, 01 | |
| 24, 0 23, 8 | 23, 9 | -3, 6 -3, 4 | 12, 96 11, 56 | 0, 1 0, 1 | 0, 01 0, 01 | |
| 24, 5 | 24, 5 | -4, 1 | 16, 81 | |||
| 25, 6 25, 4 | 25, 5 | -5, 2 -5, 0 | 27, 04 25, 00 | 0, 1 -0, 1 | 0, 01 0, 01 | |
| Всего | 367, 0 | - | 0, 1 | 239, 39 | - | 1, 98 |
Использование программы Exсel позволяет отказаться от вычисления меры линейности и коэффициента криволинейности. При подборе уравнения регрессии сравнивают R2 уравнения прямой и какой-либо кривой. Наибольшее значение R2 подскажет характер связи двух величин.
Не все изучаемые признаки можно измерить количественно. На практике часто приходится определять связь между качественными признаками, а также когда один из признаков количественный, а другой качественный.
В исследованиях по лесному хозяйству применяют коэффициенты ранговой корреляции Спирмена и Кэндалла. Расчет коэффициента Спирмена rs приведен на примере всхожести и размера семян. Пусть семена древесной породы разделены на четыре группы
(1-я, 2-я, 3-я и 4-я по размерам (крупности), а потом они же по всхожести):
| Группы семян по размерам (крупности): | ||||
Распределение групп семян по всхожести:
Разность рангов ()
Квадрат разности рангов ( ) )
| -1 |
rs= 1 – 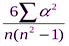 = 1 –
= 1 – 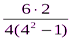 = 1 – 0, 2 = 0, 8.
= 1 – 0, 2 = 0, 8.
Связь оказалась прямой, а ее теснота – высокой.
Расчет коэффициента сходства между двумя качественными признаками. Пусть исследовано по 200 кедровых орехов, взятых в урожайный и неурожайный годы. В каждой партии подсчитано число пустых скорлупок и с орехом (табл. 4.11).
Таблица 4.11
Исходные данные для вычисления коэффициента сходства
между качеством орехов и обилием урожая
| Год | Количество орехов кедра | Всего | |
| с зародышем | без зародыша (пустых) | ||
| Урожайный | п1= 174 | п2 = 26 | N1 = 200 |
| Неурожайный | п3 = 123 | п4 = 77 | N2 = 200 |
| Итого | N3 = 297 | N4 = 103 | N = 400 |
Коэффициент сходства А равен:
A =  =
=  =
=  = 0, 29.
= 0, 29.
Основная ошибка коэффициента сходства равна:
mA = ± 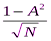 = ±
= ±  = ±
= ±  = ±0, 046.
= ±0, 046.
Достоверность коэффициента сходства t:
t = 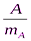 =
=  = 6, 3.
= 6, 3.
Коэффициент сходства достоверен, так как t > 4, но теснота связи качественных признаков слабая.
Кроме указанных видов корреляции, в лесном хозяйстве используют и другие (множественную, частную, чистую).
|
|