
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Табличные данные
|
|
СОДЕРЖАНИЕ
1. Задания 4
2. Краткое ОПИСАНИЕ ПАКЕТА 8
2.1 Рабочий экран программы MODELLUS 8
2.2 Примеры разработки простых моделей 10
2.2.1 Гармонические колебания 10
2.2.2 Равноускоренное движение 13
3. ПОДРОБНОСТИ 17
3.1 Работа с окнами 17
3.2 Синтаксис записи математической модели 18
3.3 Вычислительные процессы 21
1. ЗАДАНИЯ
I Пакет MODELLUS, как универсальный калькулятор
1. Установить итерационный режим работы с выполнением одного шага. В окне таблицы вывести значение квадратного корня из 2 с шестью знаками после запятой.
2. С помощью инструмента CASE организовать вычисление квадратных корней из 2, 3 и 5 (в одной модели).
3. С использованием показательной функции и инструмента CASE вычислить значения 100.5, 101.3 и 102.2. Результаты представить в экспоненциальной форме (типа 1.3456e11) с четырьмя знаками после запятой в мантиссе числа.
4. Вычислить значения sin(30o) и cos(p/4) с четырьмя знаками после запятой.
5. В неитеративном режиме создать таблицу квадратов натуральных чисел от 0 до 11. В таблице значения должны быть представлены в целочисленном формате.
6. В одной таблице представить значения функций sin(t) и cos(t) для t, изменяющегося от 0о до 30о с шагом 1о.
7. С помощью инструмента CASE составить таблицу функций sin(x) или cos(x), при х, изменяющемся от 0 до 3.14, с шагом 0.314. Использовать итерационный режим. Для переключения от синуса к косинусу в инструменте CASE воспользоваться тем, что sin(x+p/2)=cos(x).
8. Определить, при каком значении t выражение (1+1/t)t приближенно равняется неперовому числу e=2.72 (именно с двумя знаками в дробной части).
9. Вычислить функцию ex, как сумму 20 членов ряда 1+x+x2/2! +x3/3! +… Очередной член ряда вычисляется из предыдущего по формуле ai+1=ai*x/(i+1). Рассчитать e1 и e0. 5.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
10. Разработать модель, позволяющую рассчитывать факториалы целых чисел. Проанализировать, до каких значений можно считать факториал, если его значение выводится в таблицу в целочисленном формате.
11. Рассмотреть как реагирует система при выводе результатов в таблицу при «аварийных ситуациях»: извлечение квадратного корня из отрицательного числа, вычисление арксинуса от аргумента, большего единицы, деление на 0.
II Графика
12. Построить график функции y=sin(x) если х изменяется от 0 до 6p. Использовать автоматическую настройку отображения графика adjust и ручную установку пределов изменения х и у в опциях окна графика.
13. Используя инструмент CASE, построить в одном графическом окне 5 синусоид, отличающихся начальной фазой и амплитудой.
14. Проиллюстрировать графически явление биений – построить график суммы двух колебаний с одинаковой амплитудой и близкими частотами. Рассмотреть к чему приводит отличие в амплитудах колебаний.
15. Используя параметрическое задание функций, построить окружность и эллипсы с отношением осей 2: 1 и 1: 2 на одном графике.
16. Построить фигуры Лиссажу при отношении частот колебаний 1: 2, 3: 1 и 1: Ö 2 в трех графических окнах.
17. С использованием управляющей конструкции if()then() изготовить «самодельную» функции y=abs(x) и построить график функции при х изменяющемся от 1 до +1.
18. Используя средства вычисления производных вывести в одно графическое окно графики функций y(x), dy(x)/dx и d2y(x)/dx2 для функции у=х3. Графики построить в пределах –2< x< 2.
19. С помощью построения графика найти приближенное решение уравнения sin(x)=0.2 в первом квадранте. Проделать то же самое, но с использованием таблицы.
20. Построить график синусоидального сигнала, пропущенного через идеальный детектор, имеющий характеристику y(x)=x при x> =0 и y(x)=0 при x< 0.
21. Построить график синусоидального сигнала, пропущенного через квадратичный детектор, имеющий характеристику y=x2.
22. Рассмотреть как реагирует система при выводе результатов на график при «аварийных ситуациях»: извлечение квадратного корня из отрицательного числа, вычисление арксинуса от аргумента, большего единицы, деление на 0.
III Обработка данных
23. Построить график случайного процесса, в котором независимой переменной является t, а значение случайной функции задается генератором случайных чисел rnd (1), равномерно распределенных в интервале от 0 до 1.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
24. Оценить качество генератора случайных чисел, «набросав» в квадрат со сторонами 10*10 тысячу точек со случайными координатами х и у, задаваемыми генератором rnd (10). Качество генератора определяется степенью хаотичности заполнения квадрата случайными точками.
25. Найти математическое ожидание (среднее значение) 200 случайных чисел, сформированных генератором rnd (1). Воспользоваться рекуррентным соотношением Mk+1=(Mk*k+xk+1)/(k+1), позволяющим вычислить среднее для k+1 чисел через среднее для предыдущих k чисел и очередное случайное число xk+1. Убедиться в том, что среднее значение для этого генератора равно 0.5.
26. Случайные числа rnd (1)-0.5 имеют нулевое среднее значение. Тогда дисперсия N таких случайных величин x i определяется по формуле DN=Sxi2/N. Вывести рекуррентное соотношение, позволяющее вычислить дисперсию N+1 чисел через дисперсию N чисел и очередное случайное число xN+ 1. Найти дисперсию для 200 случайных чисел, сформированных указанным генератором с нулевым средним.
IV Численные методы
27. Методом деления отрезка пополам найти решения уравнений sin(x)-0.5=0 и cos(x)-0.5=0 с относительной ошибкой, не превышающей 0.001.
28. Вычислить приближенное значение определенного интеграла

методом трапеций с разбиением интервала интегрирования на 100
одинаковых отрезков.
29. Построить графики решения дифференциального уравнения dy/dx=y на интервале 0< =x< =1 при начальном значении y(x=0)=1. Найти аналитическое решение и численные решения по методу Эйлера и по методу неявной схемы.
30. С использованием метода МОНТЕ-КАРЛО вычислить значение двойного интеграла
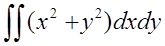
если областью интегрирования является четверть круга с радиусом 2 и с
центром в начале координат.
V Дифференциальные уравнения
31. Построить графики решения дифференциального уравнения dy/dt=-yt при начальном значении y(t=0)=1 на интервале изменения t от 0 до 3. Использовать встроенные в MODELLUS средства решения дифференциальных уравнений и аналитическое решение y=e-t^2/2.
32. Получить решение уравнения затухающих колебаний y’’ –2gy’+y=0 с начальными условиями y(t=0)=1, y’(t=0)= 0 на интервале t от 0 до 15. Необходимо преобразовать уравнение в систему двух уравнений первого порядка. Использовать встроенные средства пакета. Подобрать параметр g таким образом, чтобы на графике было четко видно затухание колебаний.
VI Моделирование физических процессов
33. Разработать модель движения тела, брошенного вверх под углом к горизонту с учетом сопротивления воздуха. С помощью графического отображения траектории подобрать начальную скорость тела (при фиксированном угле), обеспечивающую падение тела на заданную дальность.
34. Разработать модель движения тела в центральном гравитационном поле. Продемонстрировать графически возможность реализации эллиптических и параболических траекторий, в зависимости от начальной скорости.
2. КРАТКОЕ ОПИСАНИЕ ПАКЕТА
 Установка пакета на компьютер с дистрибутивных дискет или компакт-диска осуществляется стандартной для WINDOWS процедурой инсталляции. В результате на жестком диске создается каталог MODELLUS. В этом каталоге содержится подкаталог PROGRAM с запускающим программу файлом modellus.exe. Ярлык программы целесообразно поместить на рабочем столе WINDOWS, что обеспечит быстрый доступ к программе.
Установка пакета на компьютер с дистрибутивных дискет или компакт-диска осуществляется стандартной для WINDOWS процедурой инсталляции. В результате на жестком диске создается каталог MODELLUS. В этом каталоге содержится подкаталог PROGRAM с запускающим программу файлом modellus.exe. Ярлык программы целесообразно поместить на рабочем столе WINDOWS, что обеспечит быстрый доступ к программе.
2.1 Рабочий экран программы MODELLUS
После запуска программы перед пользователем открывается главное окно приложения. В верхней части окна, как обычно, располагается главное меню, содержащее, в основном, стандартные пункты:
1. File - работа с файлами. Подпункты этого пункта меню также стандартные:
a) New - создание нового файла модели. Рабочие файлы системы MODLLUS имеют расширение.mdl.
b) Open - открытие существующего рабочего файла.
c) Save - сохранение рабочего файла на жестком диске после внесения в него изменений.
d) Save as - сохранение рабочего файла под новым именем и/или на новом месте.
e) Password - создание пароля для работы с файлом.
f) Exit - выход из программы MODELLUS.
2. Edit - правка (редактирование) в рабочих окнах системы:
a) Undo - отмена последнего действия.
b) Cut - удаление выделенного фрагмента. (Выделение фрагмента производится обычными для WINDOWS способами, главным образом, с помощью манипулятора мышь.)
c) Copy - копирование выделенного фрагмента в буфер временного хранения (буфера обмена) Clipboard.
d) Paste - вставка содержимого буфера Clipboard в текущую позицию курсора ввода.
e) Copy Window - этот специфичный для MODELLUS подпункт позволяет копировать в буфер обмена целиком рабочее окно.
3. Case - варианты. Этот необычный для главного меню WINDOWS - приложения пункт позволяет системе обрабатывать одновременно несколько вариантов модели, отличающихся наборами входных параметров. Имеется два подпункта:
a) Add - добавить еще один вариант.
b) Remove Last - удалить вариант, добавленный последним.
Перед рассмотрением следующего пункта главного меню необходимо сделать остановку и поговорить о рабочих окнах программы MODELLUS. Рабочие окна открываются на фоне главного окна приложения и могут быть одного из четырех типов. Окно модели может существовать в единственном экземпляре и является, по сути дела, обычным окном простого текстового редактора. Здесь пользователь записывает, придерживаясь небольшого числа правил, формулы и уравнения, задающие математическое описание модели. Окон графиков может быть одновременно до трех. В этих окнах отображаются графики функциональных зависимостей одних переменных от других, построенные по результатам моделирования. Окна анимации (в количестве от 0 до 3) отображают результаты моделирования в виде видео клипов, которые иллюстрируют, как правило, временную эволюцию моделируемого процесса с использованием различных рисованных объектов. Наконец, окна таблиц, также в количестве от 0 до 3, могут содержать результаты моделирования в оцифрованном виде. Таблицы, анимацию и графики можно переносить в другие WINDOWS - приложения методами внедрения или связывания объектов. Следующее окно - окно параметров модели. В этом окне пользователь задает числовые значения параметров (констант), входящих в описание модели. Для моделей, базирующихся на системах дифференциальных уравнений, здесь задаются начальные условия. Кроме того, в главном окне располагается окно управления, содержащее органы запуска и остановки модели, «перемотки» моделируемого процесса вперед и назад и ряд других средств управления моделью, о которых речь пойдет в соответствующем разделе ниже.
Вот теперь можно продвигаться дальше по пунктам главного меню, следующим из которых будет:
4. Window - рабочее окно. Имеются следующие подпункты:
a) New Graph - создает очередное окно графика.
b) New Animation - создает очередное анимационное окно.
c) New Table - создает очередное окно таблицы.
d) Standard - создает некий стандартный набор рабочих окон, расположенных стандартным образом.
e) Cascade - располагает все окна «каскадом», частично наложенными друг на друга.
f) Tile - автоматически располагает окна с минимальным взаимным перекрытием.
g) Control - делает активным в текущий момент окно управления.
h) Initial Condition - делает активным окно параметров.
i) Model - делает активным окно модели, т.е. текстовый редактор.
5. Help - как обычно, пункт меню для получения помощи и справочной информации. Здесь содержатся подпункты:
a) Workshops - краткое руководство по реализации двух примеров разработки моделей. Эти примеры представлены и здесь, в конце данного раздела.
b) About Modellus - фирменная «карточка» пакета.
Необходимо отметить, что только в коммерческой версии все пункты и подпункты главного меню могут быть задействованы в полном объеме. В демонстрационной версии, которую можно получить бесплатно, невозможно, в частности, сохранять на жестком диске вновь созданные рабочие файлы и изменения в файлах примеров, поставляемых вместе с демонстрационным пакетом.
2.2 Примеры разработки простых моделей
2.2.1 Гармонические колебания.
Первый пример знакомит вас с главными особенностями создания и запуска математической модели. В этом примере вы создадите модель простого колебания с использованием тригонометрической функции SIN. Будет показано, как модель реагирует на изменения параметров. Вы также научитесь отображать результаты моделирования различными способами. Работа по созданию модели разбивается на последовательность шагов.
СОЗДАНИЕ МОДЕЛИ КОЛЕБАНИЙ.
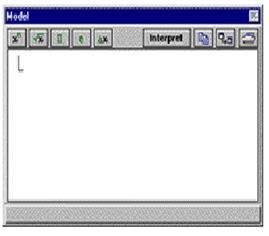 В первую очередь необходимо, конечно, запустить программу MODELLUS. После запуска программы в главном окне будут открыты три рабочих окна: окно модели, окно параметров и окно управления.
В первую очередь необходимо, конечно, запустить программу MODELLUS. После запуска программы в главном окне будут открыты три рабочих окна: окно модели, окно параметров и окно управления.
Активируйте (сделайте активным с помощью мыши или через пункт главного меню Window) окно модели. Напишите в поле редактирования окна модели формулу для простейшего случая колебательного процесса y=A*sin(w*t). Текстовый редактор системы  MODELLUS достаточно мощный, однако, он требует, чтобы вы следовали некоторым соглашениям, которые помогут системе правильно интерпретировать формулы, которые вы написали. Части уравнения или формулы, которые система воспринимает как имена переменных, будут выделены зеленым цветом, а те части, которые
MODELLUS достаточно мощный, однако, он требует, чтобы вы следовали некоторым соглашениям, которые помогут системе правильно интерпретировать формулы, которые вы написали. Части уравнения или формулы, которые система воспринимает как имена переменных, будут выделены зеленым цветом, а те части, которые 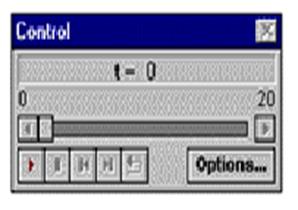 распознаются в качестве известных системе функций и математических операторов, представляются черным цветом. Так, вы ввели символ «*» в качестве знака умножения - это соответствует соглашениям системы, и символ будет изображен в черном цвете. Символ пробела также является знаком умножения. Теперь в окне модели вы будете видеть
распознаются в качестве известных системе функций и математических операторов, представляются черным цветом. Так, вы ввели символ «*» в качестве знака умножения - это соответствует соглашениям системы, и символ будет изображен в черном цвете. Символ пробела также является знаком умножения. Теперь в окне модели вы будете видеть
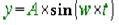
|
|
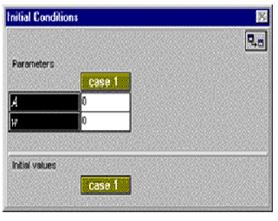
Активируйте кнопку Interpret в меню окна задач. MODELLUS транслирует формулу - подготовится к ее вычислению и отобразит в окне параметров имена тех величин, которые вы можете изменять. Активируйте окно параметров. Если это окно не вмещает список всех параметров, вы можете обычным для WINDOWS образом увеличить размер окна. Можно также менять относительные размеры двух частей окна параметров - собственно параметров и начальных условий, передвигая мышью вверх или вниз серую разделительную полоску. Введите для параметра A (амплитуды колебаний) значение 1, а для параметра w (угловой скорости) в функции SIN значение 50.
|
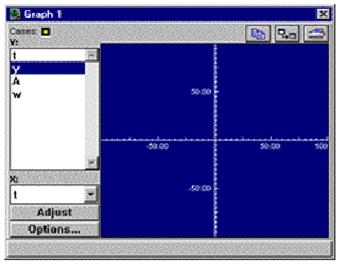
Откройте пункт Window главного меню и создайте новое (и пока единственное) окно графика - подпункт New Graph. Выберите переменную, поведение которой вы хотите воспроизвести в виде у - координаты. Для этого отметьте имя переменной в списке. Мы хотим изобразить изменения у во времени так, что если имя переменной еще не отмечено - выделите его. По умолчанию независимой переменной в MODELLUS считается время t. Поэтому в нижнем списке окна графика в качестве аргумента должна быть выбрана переменная t. Теперь в окне управления активируйте кнопку Run. Модель будет запущена на исполнение, и график будет отображаться в своем окне. Если масштабы по осям изначально не подходят для изображения графика, его будет трудно смотреть. Не печальтесь. Положение легко исправить. Активируйте кнопку Adjust окна графика, и система автоматически масштабирует изображение для наилучшего просмотра. Более того, в процессе изменения графика во времени масштабирование подстраивается под оптимальный просмотр прямо «на лету». В любой момент работу модели можно остановить активацией кнопки Stop окна управления и привести в исходное состояние кнопкой Rewind.
На самом деле, кнопки в окне управления не подписаны, а помечены условными обозначениями. Поскольку эти обозначения достаточно очевидны, мы не будем терять время на объяснения, тем более, что эти значки на кнопках привычны для пользователей бытовой аудио- и видеоаппаратуры.
Теперь следует сохранить созданную модель в виде рабочего файла. (Эта операция доступна только в коммерческой версии MODELLUS). Откройте пункт File главного меню и выберите подпункт Save. Стандартным для WINDOWS способом назначьте имя рабочему файлу и определите место сохранения.
Вы создали модель простого колебания с использованием функции SIN и отобразили поведение этой функции в зависимости от времени при заданном периоде и амплитуде. Для лучшего понимания влияния на модель значений амплитуды и угловой скорости вы можете отобразить в модели несколько вариантов ее реализации при различных значениях этих параметров. Это делается на следующем шаге.
СОЗДАНИЕ МНОГОВАРИАНТНОЙ МОДЕЛИ
|
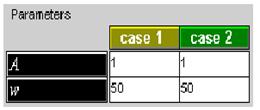
На этом шаге вы установите дополнительные варианты реализации модели и выполните их совместное отображение, позволяющее наглядно сравнивать результаты. Исходным состоянием будет предыдущая разработка. Теперь откройте пункт Case главного меню. Активация подпункта Add приведет к появлению в окне параметров дополнительного списка для тех же параметров – списки будут отличаться цветом. Первоначально,
|
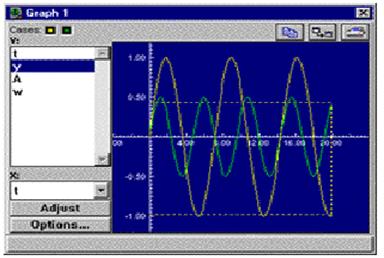
параметры для обоих случаев будут совпадать. Для второго варианта Case 2 установите значение 0.5 для амплитуды А и значение 75 для угловой скорости w. Активируйте окно графика и выберите вариант, который вы хотите отобразить на графике - маленькие цветные кнопки в верхней части окна графика, соответствующие по цвету вариантам, включают или выключают их отображения. Вы можете показать любой из вариантов или несколько вариантов сразу. Теперь запустите модель из окна управления. Если вы отображаете одновременно оба варианта, то получите в окне графика две кривые, отличающиеся цветом.
2.2.2 Равноускоренное движение.
Второй пример, который мы рассмотрим, посвящен моделированию движения тела под действием постоянной силы. В основе модели лежит второй закон Ньютона, а математическая формулировка выполнена на базе системы обыкновенных дифференциальных уравнений. С физической точки зрения модель описывает временную зависимость координат, скорости и ускорения тела в однородном поле тяжести без учета сопротивления воздуха.
СОЗДАНИЕ МОДЕЛИ.
После запуска MODELLUS необходимо активировать окно модели и записать в нем две формулы для координаты у и скорости vy тела в виде dy/dt=vy и dvy/dt=ay - каждая формула в своей строке. Редактор системы автоматически отформатирует введенные вами выражения так, что они будут выглядеть следующим образом:
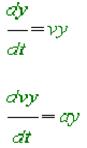
|
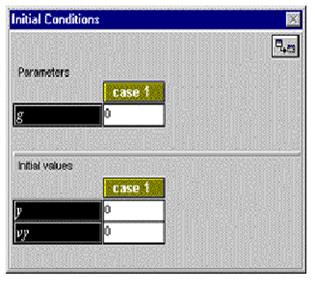
Для упрощения модели будем полагать, что на тело действует единственная сила - сила тяжести. Для тела единичной массы эта сила будет численно равна ускорению свободного падения g. Сила направлена вниз, против направления оси у. Тогда введенную систему необходимо дополнить третьим уравнением, задающим величину ускорения ay=-g.
|
В результате интерпретации модели в окне параметров, кроме полей задания параметров модели, появятся и поля начальных условий для переменных задачи. Введите значение 9.8 для величины g. Имеется в виду, что мы работаем в международной системе единиц СИ, и ускорение свободного падения равно 9.8 м/c. Введите, например, начальное значение для у, равное 375 (метров), начальное значение скорости vy задайте равным 0. Создайте новое окно графика и настройте его на построение функциональной зависимости координаты у от времени t. Теперь можно запустить модель на исполнение из окна управления. По-видимому, вам придется воспользоваться автоматическим масштабированием Adjust в окне графика. Базовая модель создана. Далее мы преобразуем график представления модели, добавим новые варианты, присоединим анимацию и отобразим результаты моделирования в числах в виде таблицы.
ПРЕОБРАЗОВАНИЕ ГРАФИКА.
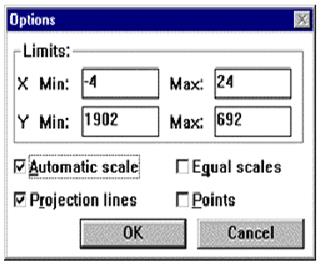
Когда вы выбираете переменные для отображения их поведения на графике, вы пользуетесь списком в левой части окна графика с полосой прокрутки. Из этого списка можно выбрать как одну, так и несколько переменных одновременно. В последнем случае выбор выполняется мышью при нажатой и удерживаемой клавише Ctrl на клавиатуре. Выделите имя vy из списка для изображения вертикальной скорости шарика в зависимости от времени. Напомним, что начальное значение скорости равно 0, и скорость линейно нарастает во времени. Нажмите и удерживайте нажатой клавишу Ctrl и при этом выделите в списке еще одну переменную у для отображения координаты как функции времени. (Если вы выделите имя у без нажатия клавиши Ctrl, то при этом выделение с переменной vy снимется.) Запустив модель при двух выделенных переменных, вы увидите в окне графика поведение во времени и координаты и скорости одновременно.
|
Вы можете установить пределы на осях графика для выделения области изменения переменных, которая представляет интерес. Так можно установить минимальное и максимальное значения на оси Y для отображения только диапазона выше поверхности (у> 0). Активируйте кнопку Option окна графика. Откроется диалоговое окно опций. Удалите отметку «Automatic scale» и введите значение 0 для минимального и значение 500 (метров) для максимального предела на оси Y. Нажмите кнопку ОК для закрытия диалогового окна. Графическое окно будет перерисовано в соответствии с новым масштабом вертикальной оси.
Теперь вы можете перенести картинку в окне графика в другое WINDOWS - приложение (только в коммерческой версии MODELLUS). Откройте пункт Edit главного меню и выберите подпункт Copy. Переключитесь в другое WINDOWS - приложение, например, в графический редактор PAINT. В этом приложении выберите пункт/подпункт Edit /Paste (или их русские аналоги) и получите перенесенную из MODELLUS картинку.
Итак, вы настроили отображение данных в графическом окне для одновариантного случая. Для лучшего понимания влияния силы тяжести, начальной высоты и начальной вертикальной скорости имеет смысл организовать многовариантное отображение с альтернативными значениями и сравнить результаты, что вам и предлагается сделать на следующем шаге.
МНОГОВАРИАНТНАЯ МОДЕЛЬ
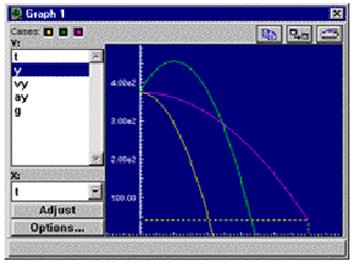
Здесь вы установите дополнительные варианты реализации модели. Во-первых, измените начальные значения вертикальной скорости и, во-вторых, измените значение ускорения свободного падения.
|
Считаем, что окно модели по прежнему содержит три уравнения, аналогично тому, как это было в предыдущем случае. Активируйте пункт/подпункт Case/Add главного меню. В окне параметров введите начальное значение 40 для переменной vy во втором варианте. Убедитесь в том, что в окне графика в списке отмечена переменная у. Обе маленькие цветные кнопки вариантов должны быть «нажаты». Запустите модель на выполнение из окна управления. В окне графики вы теперь можете видеть две функциональные зависимости координаты у от времени t для двух значений начальной скорости.
Теперь добавьте третий вариант к модели. В окне параметров для третьего варианта установите значение 1.67 для величины ускорения свободного падения g и значение 0 для величины начальной скорости vy. Нажмите маленькую кнопку вишневого цвета в окне графика для отображения и третьего варианта. Запустите модель на исполнение. Графическое окно отобразит три кривых, которые иллюстрируют интересующие нас случаи.
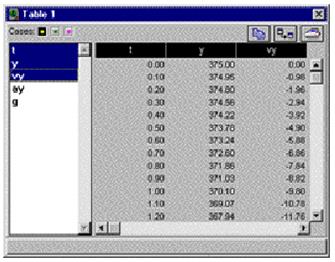
ТАБЛИЧНЫЕ ДАННЫЕ
|
Активируйте пункт/подпункт Windows/New Table главного меню. Будет создано окно таблицы, где вы должны выбрать переменную t из списка для получения столбца значений независимой переменной. При нажатой клавише Ctrl на клавиатуре выделите дополнительно имя переменной у в том же списке. К столбцу значений времени добавится и столбец значений координаты. Аналогичным образом можно сформировать, например, столбец значений вертикальной скорости, выбрав в списке переменную vy.
Может понадобиться перенести таблицу через буфер обмена в другое WINDOWS - приложение. Используйте пункт/подпункт Edit/Copy в MODELLUS, а затем Edit/Paste в другом приложении.
А теперь принимайте поздравления. Вы освоили основные приемы работы с MODELLUS! Это конечно далеко не все, что необходимо знать о программе для ее эффективного и оптимального использования, но дальнейшие сведения мы уже перенесли в следующую главу.
3. ПОДРОБНОСТИ
Хотя пакет MODELLUS разработан в соответствии с основными традициями оконного интерфейса операционных систем WINDOWS, при работе с окнами имеются некоторые особенности, на которых следует кратко остановиться.
3.1 Работа с окнами
На панели инструментов рабочих окон MODELLUS могут присутствовать кнопки копирования, скрытия и печати окна. При этом не все функции этих кнопок дублируются средствами пунктов главного меню программы.

|
Кнопка копирования окна позволяет скопировать содержимое текущего окна в буфер обмена Clipboard. Окно копируется в буфер целиком, независимо от того, какая часть содержимого была фактически открыта в рабочем окне MODELLUS. После этого содержимое буфера обмена может быть использовано любым WINDOWS- приложением, имеющим соответствующие возможности. Следует только отметить то, что содержимое всех окон копируется в графическом формате. Это относится и к окну модели, хотя может возникнуть неверное впечатление о том, что сама запись математической модели в этом окне представляет собой обычный текст.

|
Следующая кнопка предназначена для реализации возможности скрытия окна разработчиком модели от других пользователей. Такая необходимость может возникнуть, например, если пользователь не должен знать запись уравнений, описывающих модель. В этом случае разработчик делает окно модели скрытым (Hide) и после этого назначает файлу модели пароль. Для того чтобы вновь вернуть ранее скрытое окно в рабочую область необходимо открыть пункт Window главного меню и выбрать подпункт, соответствующий нужному окну.
При необходимости окончательного удаления какого-либо окна из модели следует использовать стандартную операцию закрытия окна - активировать кнопку в правом верхнем углу окна. Обратите внимание на то, что две другие стандартные для WINDOWS операции с окнами (сворачивание и минимизация/максимизация) в MODELLUS недоступны. В то же время пользователь может обычным образом перемещать окно по рабочей области, «захватив» его указателем мыши за заголовок, и изменять размеры, перемещая рамку окна. Таким образом, можно весьма гибко сконфигурировать размещение всех необходимых окон на экране.

|
Содержимое окна может быть распечатано на принтере. Для этого на панели инструментов окна имеется соответствующая кнопка. Необходимо снова иметь в виду, что на принтер будет выведено графическое изображение окна. Имеется одна особенность: вы не можете непосредственно распечатать на принтере из окна параметров значения начальных условий и параметров модели. Такой кнопки у окна параметров просто нет. Печать этих значений осуществляется из окна модели. При активации печати из этого окна вам будет предоставлена возможность выбора между моделью и параметрами. Для других окон необходимо будет просто подтвердить намерение произвести печать на принтер.
3.2 Синтаксис записи математической модели
Запись уравнений и операторов в окне модели должна подчиняться некоторым минимальным синтаксическим правилам, которые очень быстро усваиваются в процессе работы с пакетом. Нарушение этих правил выявляется при интерпретации модели, о чем система сообщит пользователю. Следует помнить, что каждое выражение должно быть написано на отдельной строке и занимать только одну строку. Отдельные части формул и выражений группируются в неразделяемые конструкции с помощью пар круглых скобок. Так, если нужно записать операцию извлечения квадратного корня из арифметического выражения необходимо вызвать символ квадратного корня (см. далее), а затем записать это арифметическое выражение, взятое в скобки. Таким же образом производится запись числителей и знаменателей дробей, если они не являются только именем переменной или числовым значением.
Любая строка записи модели может быть превращена в комментарий. Для этого в начале строки ставится символ «;», после чего эта строка не интерпретируется и является только пояснительным текстом для пользователя.
Интерпретатор модели чувствителен к регистру - различает малые и большие буквы. В этой связи принято соглашение о том, что немногочисленные служебные слова и названия функций, используемые в МODELLUS, следует набирать на нижнем регистре, малыми буквами. Что касается идентификаторов переменных, задаваемых разработчиком модели, то здесь право выбора за вами. Можно использовать любые алфавитно-цифровые комбинации, но следует избегать применения специальных символов типа «#» или «@», поскольку они могут быть зарезервированы системой.
Знаки арифметических действий записываются традиционно для всех систем программирования. Следует только иметь в виду, что знак умножения это не только символ «*», но и символ пробела. Следовательно, если вы сделали «безобидную» ошибку - случайно вставили в формулу пробел и не проконтролировали окончательное выражение, то при реализации модели вас ждет неожиданный результат.
Панель инструментов окна модели содержит пять кнопок, позволяющих вводить в набираемые формулы специальные выражения. Перечислим их в том порядке, в котором они расположены в панели:
1. Кнопка степенных функций для ввода в выражение степеней. При активации этой кнопки в формуле создаются два поля ввода для основания степени и показателя степени.
2. Кнопка квадратного корня. Вводится символ корня. Переменная или арифметическое выражение, взятое в круглые скобки, будет находиться под радикалом.
3. Число Пифагора. При нажатии этой кнопки в текущее место набираемой формулы будет вставлено значение пифагоровой константы (3.14...).
4. Эйлерова константа. Будет вставлено число Эйлера (2.71...). Обычно эта операция бывает необходимой для формирования показательной функции.
5. Символ «дельта». В выражение вводится символ соответствующей названной букве греческого алфавита. При интерпретации и запуске модели такая конструкция вычисляет приращение переменной, имя которой стоит после символа.
Вместо обращения к панели инструментов можно вызывать некоторые из перечисленных действий непосредственно с клавиатуры:
А. Степенная функция вызывается клавишей «^».
Б. Символ радикала вызывается клавишей «#».
В. Символ «дельта» вызывается клавишей «%».
Система MODELLUS имеет в своем арсенале сравнительно широкий набор математических функций, перечисленных в следующей таблице:
| Квадратный корень | sqrt() |
| Синус | sin() |
| Косинус | cos() |
| Тангенс | tan() |
| Секанс | sec() |
| Арксинус | arcsin() |
| Арккосинус | arccos() |
| Арктангенс | arctan() |
| Логарифм натуральный | ln() |
| Логарифм десятичный | log() |
| Случайное вещественное число | rnd() |
| Случайное целое число | irnd() |
| Абсолютное значение | abs() |
Аргументы функций записываются в круглых скобках после имени функции. Генератор случайных чисел при каждом к нему обращении выдает случайное число, равномерно распределенное в диапазоне от 0 до своего аргумента.
При записи математической модели имеется возможность использовать некоторые управляющие конструкции, основанные на применении служебных слов if, then, and и or. Конструкция if (условие) then (действие) работает следующим образом. Проверяется, выполнено ли условие и, если это так, то исполняется действие. Если же условие не выполнено, то действие не исполняется. Как условие, так и действие должны быть заключены в круглые скобки. В качестве условий может использоваться одна или несколько операций сравнения. Синтаксис написания операций сравнения и смысл операций представлены в следующей таблице:
| A==B | A равно B |
| A< > B | A не равно B |
| A> B | A больше B |
| A< B | A меньше B |
| A> =B | A больше или равно B |
| A< =B | A меньше или равно B |
В качестве действия обычно используется операция присвоения значения какой-либо переменной. Так, например, конструкция if (x> =0) then (y=4) выполнит присвоение переменно у значение 4, если переменная х имеет неотрицательное значение. Если же значение х отрицательно, никакого действия с переменной у не производится. Условия могут быть объединены операциями логического умножения and (логическое И) и логического сложения or (логическое ИЛИ). Так управляющая конструкция if ((a > 3) and (a < 4)) then (M=122) выполнит присвоение переменной М значения 122 в том и только том случае, если значение переменной а лежит в интервале от 3 до 4.
Конструкция if ((a< 3) or (a> 4)) then (M=122) наоборот присвоит переменной М это значение в том и только том случае, когда переменная а напротив находится вне интервала от 3 до 4.
Операция логического умножения может использоваться не только для объединения условий, но и для объединения действий. Выражение if (p< > 0) then ((s=1) and (g=2)) предписывает выполнение двух действий - присвоения значений переменным s и g в том случае, если переменная р не равна нулю. Для написания цепочки действий, в результате которых переменная у получит значение абсолютной величины переменной х, можно создать две строки в окне модели:
if (x> =0) then (y=x)
if (x< 0) then (y=-x)
Разумеется, практически в такой последовательности никакой необходимости нет, поскольку в нашем распоряжении имеется стандартная функция вычисления модуля.
3.3 Вычислительные процессы
 Пакет MODELLUS, как это уже должно быть понятно читателю, предназначен для исполнения двух основных задач компьютерного моделирования. Первая заключается в выполнении всех необходимых вычислений для реализации математической модели. Вторая задача связана с адекватным представлением результатов моделирования и обеспечением модели удобными средствами управления ею. В данном разделе более подробно рассматриваются вычислительные возможности пакета.
Пакет MODELLUS, как это уже должно быть понятно читателю, предназначен для исполнения двух основных задач компьютерного моделирования. Первая заключается в выполнении всех необходимых вычислений для реализации математической модели. Вторая задача связана с адекватным представлением результатов моделирования и обеспечением модели удобными средствами управления ею. В данном разделе более подробно рассматриваются вычислительные возможности пакета.
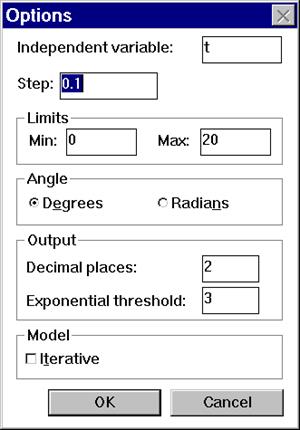
Прежде всего, следует отметить, что пакет может работать в одном из двух режимов, задаваемых соответствующей опцией окна управления. В обычном (не итеративном) режиме, принятом по умолчанию, считается, что моделируемый процесс развивается во времени так, что независимой переменной является переменная t,. изменяющаяся от 0 до 20 с шагом 0.1. Имя независимой переменной, пределы ее изменения и шаг могут быть изменены пользователем произвольным образом. Этот режим используется тогда, когда математическая модель предполагает решение дифференциальных уравнений с производными по независимой переменной.
Заметим попутно, что в окне опций можно установить способ задания углов как аргументов тригонометрических функций - радианный или градусный. Здесь же задается количество выводимых цифр после десятичной точки в дробной части числа, представляемого в окне таблиц - Decimal places. Значение в поле Exponential threshold задает порядок числа, начиная с которого величина выводится в экспоненциальном представлении: мантисса, умноженная на степень десяти. Если здесь стоит 0, то данные всегда выводятся в экспоненциальном формате.
Второй режим, названный итеративным (устанавливается меткой Iterative при настройке опций окна управления), реализует многократное циклическое исполнение последовательности действий, записанных в окне модели. Количество циклов выполнения этой последовательности задается в опциях управления конкретным целым числом. Итеративный режим не предусматривает (и, более того, запрещает) автоматическое решение дифференциальных уравнений, хотя разработчик может «вручную» записать в окне модели реализацию соответствующего численного метода. При этом никакой независимой переменной программа не создает, и относящиеся к ней установки опций в окне управления будут не активируемыми. Уже из названия режима понятно, что он предназначен для реализации вычислений по итеративным схемам. Типичными применениями такого режима могут являться метод последовательных приближений для самых разнообразных задач, метод Ньютона для поиска корней уравнений, вычисление сумм последовательностей.
Процесс обработки не итеративной модели начинается с того, что система пытается найти конструкции, соответствующие записи систем дифференциальных уравнений. MODELLUS решает задачи Коши (начальные задачи) для систем обыкновенных дифференциальных уравнений первого порядка. Если вам необходимо, например, получить решение уравнения третьего порядка, то его необходимо известными способами превратить в систему трех уравнений первого порядка. Система должна быть разрешена относительно первых производных так, что в записи системы в окне модели производные (и только они) должны находиться в левых частях выражений присваивания. В правых же частях производные не должны присутствовать. Примеры формирования и записи систем дифференциальных уравнений даны в предыдущих и последующих разделах.
После успешной интерпретации модели система подготавливает к выполнению (но до запуска модели на исполнение не выполняет) численный алгоритм решения. В качестве такового MODELLUS использует схему Рунге-Кутта четвертого порядка без автоматического выбора шага. Следует отметить, что точность решения в первую очередь зависит от выбора шага интегрирования. Во многих случаях принятый по умолчанию шаг изменения независимой переменной, равный 0.1, не обеспечивает необходимой точности. В этом случае необходимо подобрать меньший шаг, используя установку опций окна управления. В результате интерпретации в окне параметров появляются поля для ввода значений, соответствующих начальным условиям задачи Коши. Начальные условия должны задаваться только числовыми константами. Теперь часть модели, описываемая дифференциальными уравнениями, готова к реализации. Процесс вычислений по схеме Рунге-Кутта реально начнется после того, как вы запустите модель на выполнение. При этом вы получаете решение уравнений как функции времени с шагом, заданным опциями управления. Решение заканчивается по достижению времени, указанного в тех же опциях. Возможно ли «досрочное» прекращение расчетов? Да. Во-первых, можно приостановить или полностью прервать процесс из окна управления. Во-вторых, поместив в описание модели управляющую конструкцию типа if (y< 0) then (t=20), вы можете проинструктировать модель об автоматическом прекращении работы, как только переменная у станет отрицательной - предполагается, что в опциях управления задан верхний предел для t, равный 20.
Все остальные строки записи модели должны представлять собой либо выражения присваивания для каких либо переменных, либо управляющие конструкции. Эти элементы выполняются в той последовательности, в какой они записаны. Окончательная интерпретация модели определяет, какие значения переменных в данной записи остаются неопределенными. Они рассматриваются как параметры (входные данные) модели и появляются в окне параметров. Как и для начальных условий, параметрам должны быть приданы числовые значения. По умолчанию все параметры и начальные значения обнуляются, что можно видеть в окне параметров сразу после интерпретации модели. В следующем разделе будет подробно показано, как параметры модели (но не начальные условия) можно менять в процессе работы модели из окон анимации.
В процессе выполнения расчетов могут возникнуть разного рода аварийные ситуации. Реакция системы на попытку деления на 0 довольно непредсказуема, поскольку зависит от того, в каких условиях это произошло. Более благополучно дело обстоит с попыткой извлечения квадратного корня из отрицательного числа. Ничего страшного при этом не произойдет - даже не прервется процесс вычислений. Однако если в окне таблиц предполагается вывод значения с таким конфузом, то на этом месте будет просто пропечатан дефис. В графических окнах при этом будет прорисован знак радикала.
Некоторые дополнительные возможности открываются при использовании упоминавшегося выше символа D. Выражение Dt имеет численное значение шага изменения независимой переменной - того самого, которое задается опциями окна управления. Применение этой конструкции позволяет, в частности, автоматически учитывать величину шага при записи модели, когда вы меняете его значение.
В программу встроена возможность численного определения производных функций. Если, например, в модели есть последовательность выражений: y = sin (x) z=dy/dx, то переменная z будет иметь численное значение, равное cos (x), подсчитанное при текущем значении х. Здесь необходимо отметить один важный момент. Операции с производными допустимы только в обычном (не итеративном) режиме. Попытки использования производных, включая решения дифференциальных уравнений, в итеративном режиме вызывают диагностирование ошибки на этапе интерпретации модели.
Как уже говорилось, в итеративном режиме количество циклов расчетов по модели строго фиксировано. В ряде случаев это ограничение нежелательно. Например, поиск корня уравнения методом Ньютона можно прекратить либо после выполнения 100 итераций или когда значение функции при значении очередного приближения корня по абсолютной величине станет меньше заданной величины. Для первого случая подходит итеративный режим, а вот второй вариант в этом режиме реализован быть не может.
Практикум «Пакет MODELLUS»
|
|
