Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Введение. Многие современные задачи, которые решает наука о материалах, не поддаются исследованию в нужной полноте и точности обычными теоретическими и

Многие современные задачи, которые решает наука о материалах, не поддаются исследованию в нужной полноте и точности обычными теоретическими и экспериментальными методами. Прямые натурные эксперименты слишком длительны (например, в реакторном материаловедении), дороги, часто опасны или попросту невозможны (поведение материалов в аварийных ситуациях). Как следствие, за последние 20 лет вычислительная физика приобрела статус независимого мощного методологического направления в области исследования материалов наряду с экспериментальной и теоретической физикой. Современной тенденцией стало активное сближение экспериментальной и вычислительной физики, и все чаще эксперимент и моделирование становятся взаимодополняющими частями одного исследования.

Моделирование какого-либо объекта или явления методами вычислительной физики требует четкой постановки задачи с последующей разработкой самосогласованного плана действий. Типичный план действий условно состоит из трех основных этапов (формулировка академика А.А. Самарского): «модель – алгоритм – программа» (см. рис. 14.1).

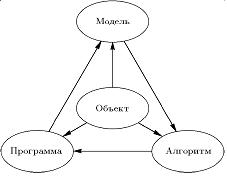
Рис. 14.1. «Триада» метода математического моделирования

На первом этапе формулируется «эквивалент» изучаемого объекта или явления, отражающий в математической форме важнейшие его свойства – законы, которым он подчиняется, связи, присущие составляющим его частям, и т. д. Второй этап заключается в выборе (или разработке) алгоритма для реализации модели на компьютере. Модель представляется в форме, которая удобна для применения численных методов и определяет последовательность вычислительных и логических операций, которые нужно произвести, чтобы найти искомые величины с заданной точностью. Вычислительные алгоритмы не должны искажать основные свойства модели, быть экономичными и адаптирующимися к особенностям решаемых задач. На третьем этапе создаются программы, «переводящие» алгоритм на доступный компьютеру язык. Их можно назвать электронным эквивалентом изучаемого объекта, уже готовым для испытания на «экспериментальной установке» - компьютере (проведение «компьютерного эксперимента»).

Создав триаду «модель-алгоритм-программа», исследователь получает универсальный, гибкий и сравнительно недорогой инструмент, который вначале отлаживается в пробных компьютерных экспериментах. После того как достаточное соответствие модели исходному объекту установлено, с моделью можно проводить разнообразные и подробные компьютерные эксперименты, дающие требуемые качественные и количественные свойства и характеристики объекта. Процесс компьютерного моделирования сопровождается улучшением и уточнением, по мере необходимости, всех элементов триады.

Компьютерное (численное) моделирование как метод исследования можно представить в виде цепочки последовательно связанных элементов: «исследуемое явление – математические модели – численные алгоритмы – программирование – вычисления на компьютере – анализ результатов». Для различных задач отдельные элементы этой цепочки могут быть объединены или пропущены.

Широкое использование компьютерного моделирования обусловлено многими факторами, основными из которых являются:

· усложнение исследуемых задач, решение которых в рамках чисто экспериментального подхода затруднительно, либо требует создания дорогостоящих установок;

· невозможность проведения в ряде случаев натурного моделирования;

· сокращение сроков и снижения затрат на проведение исследований и получение результатов.

Компьютерное моделирование не подменяет собой математику, физику и другие научные дисциплины. Наоборот, оно играет синтезирующую роль, опираясь на самые разные методы и подходы – от анализа нелинейных моделей до современных методов алгоритмизации процессов, и дает дополнительные стимулы развития самым разным направлениям науки. Использование компьютерного моделирования в решении задач современной науки о материалах дает возможность эффективно разрабатывать высокотехнологичные, конкурентоспособные современные материалы и технологии их получения.