Представление пространства поиска.

Поиск представляет собой комплекс действий, выполняемый поисковой системой (ПС) в процессе преследования цели. Комплекс действий включает последовательное выполнение следующих процедур:

1) «генерации» возможных или ограниченных априорной и/или апостериорной информацией о пространстве поиска решений;

2) «проверки» результатов генерации (идентификации полученных решений с целью поиска, их последующие хранение, учет, ранжирование и т.д.);

3) «планирование» способа достижения цели.

Организацию пространства состояний удобно представить в виде ориентированного графа (орграфа), где множество его вершин сопоставимо с состояниями, а множество дуг -сопоставимы с операторами, преобразующими состояния множества.

Представление пространства состояний в виде орграфа позволяет выделить дополнительные свойства и организацию состояний. Свойстваопределяются отношением подмножеств, входящих и выходящих дуг.

Рассмотрим условия соотношений множеств Yⁱⁿ { y_j } (входящих дуг) и Y^out { y_j } (выходящих дуг), устанавливающие организацию орграфа G: Если для всякой вершины x_iÎ X орграфа G, выполняются условия: ç Yⁱⁿ { y_j }ç = n-1 и ç Y^out { y_j }ç =n- 1, то орграф представляет собой замкнутую структуру.

Пространство поиска в составе пространства состояний образуется за счет обобщения видовых признаков некоторых состояний. В этом случае обобщенные видовые признаки дополняют множество родовых признаков данных состояний, образуя собственное пространство поиска в пространстве состояний или класс состояний.

Каждое состояние пространства состояний получено прямым или обратным преобразованием.

Глубина пространства поиска меньше либо равна n-1, где n-число цифр в состоянии.

Элементы пространства поиска различны.

Между пространством состояний и пространством поиска существуют следующие отношения: 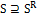и |S | ≥ 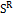. Пространство поиска в составе пространства состояний образуется за счёт дальнейшего обобщения видовых признаков некоторых состояний.

В результате обобщенные видовые признаки дополняют множество родовых признаков данных состояний, образуя собственное пространство поиска в пространстве состояний или класс состояний.

Процесс решения задачи в дискретном пространстве может быть представлен как последовательный переход из одной дискретной точки пространства (состояния) в другую. Множество всех дискретных состояний образует дискретное пространство состояний (далее просто пространство состояний): S = { s 1, s 2, …, sm }, где m  количество всех состояний множества S. Всякое состояние si  S характеризуется множеством признаков K = { k 1, k 2, …, kn }. Среди множества признаков состояний следует вы-

делить:

1) подмножество родовых признаков состояний KR  K, характери-

зующее всякое состояние пространства состояний. Подмножество родовых

признаков формируется путем выделения тождественных признаков, пред-

ставляющих состояния. Родовые признаки, по сути, выделяют подмноже-

ство состояний из множества состояний, т. е. выполняется условие KR  .

Состояния, принадлежащие подмножеству, составляют уникальное дочер-

нее подпространство состояний;

2) подмножество видовых признаков состояний KV  K выделяет

всякое состояние пространства состояний. Для всякого состояния про-

странства состояний выполняются следующие условия: KV   и KV 

уникально; иначе, будет иметь место такой случай: si  sj  одно со-

стояние.

В качестве примера рассмотрим следующие состояния: s 1(ki, kj, ka, kb),

s 2(ki, kj, ka, kс), s 3(ki, kj, kc, kb) и s 4(kd, kf, kg). Отметим, что состояния s 1, s 2 и s 3

§ 1.3. Пространство состояний

в отличие от состояния s 4 обладают общими признаками ki и kj. Признаки ki

и kj образуют множество KR, следовательно, состояния s 1, s 2 и s 3 составляют

пространство состояний. Признаки ka, kb являются видовыми для состоя-

ния s 1, ka, kc  для состояния s 2 и kc, kb  для состояния s 3, т. е. составляют

множества KV данных состояний.

Кроме иерархического отношения «род – вид» пространство состоя-

ний можно охарактеризовать отношением «часть – целое»:

S = 

N

i  1

Si,

где Si  подмножества множества S.

Причем должно быть выполнено условие

 N

i  1

Si  .

Отношение «часть – целое» обуславливает то, что пространство со-

стояний включает в свой состав:

1) подмножество So начальных состояний. Это подмножество со-

стояний, из которых осуществляется начало поиска. Для данного подмно-

жества выполняется условие So  . Начальные состояния характеризуют

актуальное состояние системы;

2) подмножество St целевых состояний. Это подмножество состояний

представляет собой множество решений задачи или цель поиска. Для дан-

ного подмножества выполняется условие St  ;

3) подмножество Sс текущих состояний. Для данного подмножества

обычно выполняется условие Sс   (в некоторых случаях Sс формируется

за счет состояний множеств So и St).

При выполнении условий Sс = , пунктов 1 и 2 и условия so

i  fg = st

j,

где fg  оператор преобразования so

i  So в состояние st

j  S t, достижение

целевого состояния выполняется в одно действие. В этом случае, как уже

отмечалось, задача является элементарной, и поиска как такового не вы-

полняется. В данном контексте простой задачей будем считать случай, ко-

гда ПС известна цепочка операторов Li = (f 1, f 2, …, fn), применение которой

к состоянию so

i позволяет перейти в состояние st

j  S t. Причем  Li   1 и

соответственно Sс  .

Важным понятием, используемым при решении задач в пространстве

состояний, является понятие пространство поиска – SR. Необходимость

Глава 1. Поиск, задачи поиска и пространство состояний

введения понятия SR продиктовано прежде всего ситуациями, когда про-

странство состояний состоит из нескольких несвязных подпространств со-

стояний, каждое из которых представляет собственное пространство поис-

ка. Примером тому являются пространства состояний в задачах, представ-

ленных в прил. А, Б.

В отличие от пространства состояний для пространства поиска вы-

полняется следующее условие.

Для любой пары состояний (si, sj)  SR всегда найдется одна и более

цепочек операторов Li = (f 1, f 2, …, fn), применение которой к состоянию si

приведет к состоянию sj. Причем все текущие состояния, представляющие

некоторый путь от состояния si до состояния sj, также будут принадлежать

данному пространству SR. Следовательно, множество SR – это всегда связ-

ная область.

Между пространством состояний и пространством поиска сущест-

вуют следующие отношения: S  SR и  S    SR . Пространство поиска в

составе пространства состояний образуется за счет дальнейшего обобще-

ния видовых признаков некоторых состояний. В результате обобщенные

видовые признаки дополняют множество родовых признаков данных со-

стояний, образуя собственное пространство поиска в пространстве состоя-

ний или класс состояний.

В качестве примера рассмотрим состояния: s 1(ki, kj, ka, kb), s 2(ki,

kj, ka, kс) и s 3(ki, kj, kc, kb), образующие пространство состояний на ос-

нове общих признаков ki и kj. Анализируя состав видовых признаков

состояний, можно отметить, что состояния s 1 и s 2 имеют общий при-

знак ka, состояния s 2 и s 3 – признак kc и s 1, s 3 – признак kb, позволяю-

щие организовать собственные пространства поиска или подклассы

состояний SR. __

Для реализации игры также необходимо учесть, то обстоятельство, что при догонном виде преследования, скорость движения ПС должна быть выше скорости движения цели. Для этого необходимо в работу программы имитирующей классическую погоню алгоритмов А*, внести изменения связанные с этим условием. Так необходимо, чтобы алгоритм А* имитирующий работу ПС выполнял большее количество итераций, иначе ему сложно будет догнать цель. В практическом варианте программы моделирующей классический алгоритм погони следует обеспечить возможность задания «скорости» работы ПС относительно скорости движения цели. Например, для ПС скорость (количество выполняемых итераций) относительно алгоритма имитирующего движение цели, можно задать соотношением в два и более раз. Для имитации работы классического алгоритма погони скорость ПС на всем протяжение поиска цели обычно остается постоянной.

Следует отметить, что в практической программе погони в этих условиях для имитации работы ПС следует использовать модернизированный алгоритм А* с памятью. Память в модернизированном алгоритм А* можно использовать в разных качествах. Например, отслеживать случаи попадания ПС в кольцо, при необходимости выполнять процедуру back-track и т.д. При этом основным назначением памяти является отображение «кривой погони». Анализ результатов преследования (кривой погони) позволяет оценить особенность движения в пространстве поиска алгоритма имитирующего работу ПС. При промахе алгоритм ПС может выполнить несколько маневров вокруг цели. Величина и количество, которых будет зависеть от соотношения скоростей ПС и цели и конечно от мощности испытываемой последовательности.

В современных ПС различного назначения классический вариант алгоритма погони применяется только в модернизированном виде. Обычно современный вариант организации классической погони применяется в условиях погони за прямолинейно движущейся целью, на острых углах и главное с переменной скоростью ПС. Корректировка скорости ПС происходит за счет анализа изменения расстояния между ПС и целью. И все же формируемый классическим алгоритмом путь далек от оптимального вида даже с учетом возможности корректировки скорости движения ПС при приближении к цели.

Представить работу алгоритма преследования с упреждением можно также на примере задачи «перестановка». В качестве цели и ПС также используются алгоритмы А*. Отличие работы алгоритма ПС с упреждением будет заключаться в том, что в качестве целевых состояний следует задать множество дочерних состояний образуемых некоторым текущим состоянием цели при движении из пункта А в пункт Б. В этом случае моделируется выполнение условия преследования с упреждением. В процессе преследования алгоритм А* имитирующий работу ПС будет всегда нацелен на дочернее состояние ближайшее к пункту Б, текущего положения алгоритма А* моделирующего движение цели.

Таким образом необходимо в работе алгоритм А* имитирующего погоню ПС предусмотреть возможность выполнения опережающего преобразования текущей последовательности цели. Глубина такого анализа должна быть ограничена заданным ресурсом опережающего анализа связанным с соотношением скоростей и мощностью пространства поиска (колец графа), т.е. некоторой эвристической системной оценкой из состава оценочной функции ПС.