Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критерії та методи кластеризації
|
|
Практичні класи комбінаторних задач розпізнавання образів вимагають значних часових затрат через розмірність задач та складність описів самих образів. Скоротити їх можна шляхом виділення основних особливостей моделей, врахування менш суттєвих параметрів на пізніших етапах обчислень, детального пошуку в стратегічно важливих напрямках та менших розмірностях шуканих об’єктів.
Кластеризація як специфічний засіб класифікації об’єктів застосовується до скінченої множини об’єктів. Відношення між об’єктами представляються симетричною матрицею суміжностей, елементи якої є характеристиками подібності, несхожості, сусідства тощо. Ці характеристики набирають конкретних значень, якщо об’єктами є образи для розпізнавання, точки в n -мірному просторі тощо. Зокрема, ними можуть бути віддалі в Евклідовому просторі, пропускна провідність між об’єктних елементів тощо. Фізичний зміст матриці відповідає змісту кластерного аналізу, математична матриця є вхідними даними для алгоритмів кластеризації..
Нехай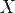 
— множина об'єктів, 
— множина номерів (імен, міток) кластерів. Задано функцію відстані між об'єктами 
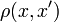. Є кінцева вибірка об'єктів 
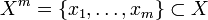. Потрібно розбити вибірку на непересічні підмножини, що називаються кластерами, так, щоб кожен кластер складався з об'єктів, близьких по метриці 
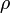, а об'єкти різних кластерів істотно відрізнялися. При цьому кожному об'єкту 
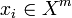приписується номер кластера 
.
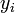Алгоритм кластеризації — це функція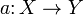 
, яка будь-якому об'єкту 
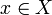ставить у відповідність номер кластера 
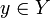. Множина в деяких випадках відома заздалегідь, проте частіше ставиться завдання визначити оптимальне число кластерів, з погляду деякого критерію якості кластеризації.
Відомо, що графічні образи Оі (відбитки пальців, знімки внутрішніх органів, фотознімки людей тощо) займають значне місце в пам’яті і їх використання як ключів для пошуку необхідної інформації для співставлення заданого і шуканого ключів (розпізнавання образів) потребує значного часу. Тому для прискорення пошуку характеристик заданого образу застосуємо два прийоми: 1) контекстуальний - заміна графічного образу множиною характеристичних його ознак, 2) датологічний – групування ключів з допомогою ієрархічного дерева формування кластерів образів. Кластери – це образи, характеристики яких близькі між собою згідно певного критерію. Тоді задача зберігання та пошуку образів містить наступні етапи: знаходження характеристичних ознак та формування на їх основі ключів, формування дерева кластерів, грубе оцінювання позиції ключа в списку, точне співставлення ключів образів або самих образів. Кількість операцій порівняння в даному випадку значно менша за рахунок меншої кількості ключів. Групування образів як ключів в чисто графічному зображенні з їх сукупностями інтегральних оцінок є надзвичайно складною задачею. Тому для кожного образу заданого типу виділяються групи характеристичних параметрів, які можуть бути прийняті за проміжні ключі образів для швидкого їх опрацювання. Найшвидше опрацювання можливе, якщо ключі будуть погруповані з допомогою оптимального збалансованого дерева [3].
Згідно з [3], поділ алгоритмів кластеризації фактично зводиться до поділу на 2 типи алгоритмів – ієрархічні алгоритми (hierarchical – методи перетворення матриці віддалей в послідовність груп поділу) та алгоритми розбиття (partitional – один раз роблять поділ з метою відновлення справжніх груп, які присутні у даних).
Призначення алгоритмів об'єднання (їх називають деревовидною кластеризацією - результатом є ієрархічне дерево [6].) полягає в об'єднанні об'єктів в достатньо великі кластери, використовуючи деяку міру схожості або відстань між об'єктами.
Міра схожості між кластерами обчислюється у два етапи: міра схожості між складовими об’єктамирізних кластерів та на їх основі міра схожості між кластерами.
Евклідова відстань - найбільш загальний тип відстані між об’єктами. Вона є геометричною відстанню в багатовимірному просторі і обчислюється таким чином:
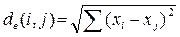(1.1)
Евклідова відстань обчислюється за початковими даними. Її перевагами є незалежність від введення в аналіз нового об'єкту. Проте, на відстані впливають відмінності між осями, за координатами яких обчислюються ці відстані. Наприклад, якщо одна з осей виміряна в сантиметрах, а потім в міліметрах, то остаточно евклідова відстань зміниться, і, як наслідок, результати кластерного аналізу можуть сильно відрізнятися від попередніх.
Манхеттенська відстань. Ця відстань є сумою абсолютних різниць координат різних об’єктів. Вона обчислюється за формулою:
(1.2)
Статична відстань. Для збільшення або зменшення ваги різниць координат використовують статичну відстань, яка обчислюється за формулою:
, (1.4)
Відстань Чебишева. Якщо віддається перевага одній координаті, то відстань обчислюється за формулою:
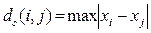(1.3)
Приклади двох кластерів з їх об’єктами представлено на рис.1.2. Обчислення відстаней між кластерами потребує вибору типу відстані між об’єктами, пошуку об’єктів- представників кластерів та обчислення відстаней для них. Існують різні підходи до формування відстаней схожості між кластерами.
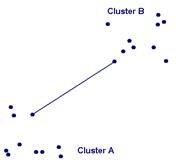
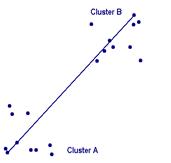
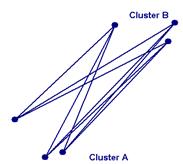
Одинарний зв'язок (single link - метод найменш віддалених сусідів). У цьому методі відстані між кластерами визначаються найменшою відстанню між будь-якими двома об'єктами в різних кластерах (тобто “найменш віддаленими сусідами”). Цей метод придатний длят кластерів, що мають подовжену форму або їх природний тип є “ланцюжковим”.
Відстань між кластерами D(r, s) приймають як
D(A, B) = min { d(i, j): об’єкт i є у кластері A а об’єкт j – у B }
Повний зв'язок (complete link - метод найбільш віддалених сусідів). У цьому методі відстані між кластерами визначаються найбільшою відстанню між будь-якими двома об'єктами в різних кластерах (тобто “найбільш віддаленими сусідами”). Цей метод зазвичай працює дуже добре, коли об'єкти насправді походять з різних груп. Якщо ж кластери мають в деякому роді подовжену форму або їх природний тип є “ланцюжковим”, то цей метод непридатний. Відстань між кластерами D(r, s) приймають як
D(A, B) = max { d(i, j): об’єкт i є у кластері A а об’єкт j – у B }
Незважене попарне середнє. У цьому методі відстань між двома різними кластерами обчислюється як середня відстань між всіма парами об'єктів в них. В роботі [7] для метода вводять абревіатуру UPGMA (unweighted pair-group method using arithmetic averages).
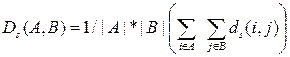
об’єкт i є у кластері A а об’єкт j – у B
Зважене попарне середнє. В методі при обчисленні використовується ваговий коефіцієнт на основі кількості об’єтів у кластері. В роботі [7] для метода вводять абревіатуру WPGMA (weighted pair-group method using arithmetic averages).
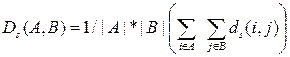
об’єкт i є у кластері A а об’єкт j – у B
Незважений центроїдний метод. У цьому методі відстань між двома кластерами визначається як відстань між їх центрами ваги. В [7] використовується абревіатура UPGMC (unweighted pair-group method using the centroid average).
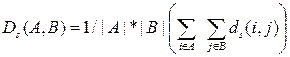
об’єкт i є у кластері A а об’єкт j – у B
Зважений центроїдний метод (медіана). При обчисленнях використовуються ваги для врахування розмірів кластерів (кількості об'єктів в них). В [7] автори використовували абревіатуру WPGMC (weighted pair-group method using the centroid average).
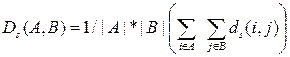
об’єкт i є у кластері A а об’єкт j – у B
Метод Варда. Цей метод відрізняється від всіх інших методів, оскільки він використовує методи дисперсійного аналізу для оцінки відстаней між кластерами. Метод мінімізує суму квадратів для будь-яких двох (гіпотетичних) кластерів, які можуть бути сформовані на кожному кроці. Детальніше метод розглянутий в [8], ефективним, використовується для створення кластерів малого розміру.
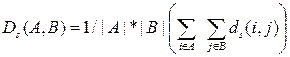
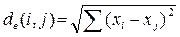
об’єкт i є у кластері A а об’єкт j – у B
Об”єкти, призначені до зберігання, представимо множиною Q (Q 1, Q 2, Q 3 , …, QN), де N – достатньо велике значення. Кожному об’єкту притаманні певні характеристичні ознаки a, b, c, … (розміри, координати центра тощо), які виражаються числовими значеннями. Тобто кожному об’єкту ставиться у відповідність множина його характеристик Q 1 = Q 1(а 1, b 1, c 1, …), Q 2 = Q 2(а 2, b 2, c 2, …), Q 3 = Q 3(а 3, b 3, c 3, …), …, QN = QN (аN, bN, cN, …). Для прискорення пошуку відповідного об’єкту (групи) у списку об’єктів останні згрупуємо, зафіксувавши місце розташування групи на дереві. Групи об’єктів відповідають кластерам, утвореним за певними критеріям близькості на основі дерева згортання зображення [112, 113].
Кластеризація здійснюється процедурою, на i -му кроці якої формується множина Хi+ 1вершин дерева, і представляється так:
(2.1)
\ 
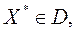
(2.2)
де D – клас допустимих рішень, а множина Вi утворюється на основі новоутворених вершин, які задовольняють найкращим значенням функції критерію F (X*). Крім того, в цю множину входять вершини множини Сі попереднього рівня, які не об’єднувались, тобто:
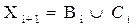. (2.3)
Об’єднання двох кластерів відбувається, якщо функція для них приймає мінімальне значення:
F* = min (Fk j), k, j Î I, (2.4)
де I – множина всіх можливих пар початкових об’єктів, кластерів та їх комбінацій. Зауважимо, що новоутворені кластери позначаємо також символом QN+k з індексом, більшим за початковцу кількість об’єктів N.
Процедуру реалізує наступний алгоритм:
Крок 0. Для всіх точок xi, xj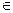 
X.
Крок 1. Пошук пар кандидатів за функцією подібності:
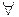(xi, xj (j > i)) підрахунок F (xi , xj). (2.5)
Крок 2. Пошук пар, що мають найменше значення відстані
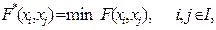(2.6)
cтворення нової точки (кластера) xn +1 об’єднанням точок xi, xj.
Крок 3. Видалення точок xi, xj зі списку кандидатів.
Крок 4. Кінець (для всіх xi, xj 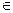X).
Для найкращої точності універсальний ієрархічний алгоритм характеризується поліноміальною складністю O (N 3). Для зменшення складності до O (N 2) автори в [114] пропонують знайти так званих друзів об’єднаних на однаковому рівні дерева. Зауважимо, що автори не пояснюють витрати, необхідні для знаходження найменших відстаней для всіх друзів на кожному рівні дерева.
Відтань d(i, j) утворимо як зважену суму модулів різниць (манхеттенської відстані) (на відміну від 2..3) між характеристиками кластерів, що є кандидатами на об’єднання в один спільний кластер:
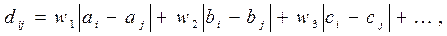(2.7)
або як зважену суму квадратів різниць між характеристиками:
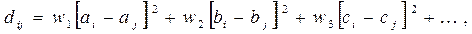(2.8)
де сумування відбувається за всіма ознаками, які формують ключ образу.
Введенням зваженої функції критерію підкреслюємо факт, що задача поділу об’єктів у кластери розв’язується як задача багатокритеріальної оптимізації методом згортання декількох критеріальних функцій в одну.
Важливим питання є масштаб значень ознак об’єктів аi, bi, ci, ..., на основі яких формуються кластери. Без врахування масштабу чисел значення менших порядків будуть знівельовані найбільшими числами. Тому кожне з значень ознак має нормалізуватись розкидами можливих значень, наперед заданих.
Вхідні дані нормалізовані за наступною формулою:
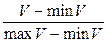(2.9)
Спочатку експерименти були проведені для підтвердження адекватності функції до оцінювання точності алгоритму
Далі вважаємо, що значення ознак об’єктів нормалізовані.
В процесі побудови дерева утворюються характеристики новоутворених вершин за простим усередненням характеристик складових вершин:
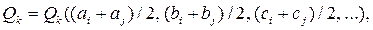(2.10)
або за зваженим усередненням характеристик складових вершин для врахування розмірності кластера – претендента на об’єднання:
(2.11)
де k, r – кількості характеристик у i -ому, j -ому кластерах – вузлах дерева згортання.
Якщо не передбачити критерію зупинки, то в результаті роботи алгоритму будується повне дерево з однією вершиною – коренем (приклад на рис. 1.1).
. 
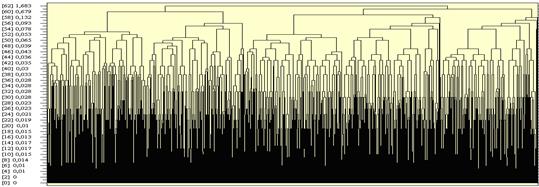
Рис. 1.1. Дендрограма згортання вибірки 5000 точок
Для побудовано дерева згортання на рис. 1.2 представлено залежність функції схожості від рівня згортання кластерів.
|
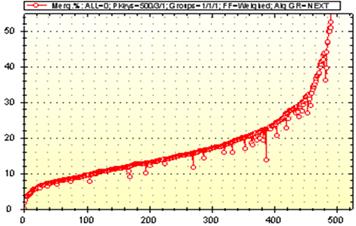
Рис. 1.2. Функція сусідства при згортанні вибірки 5000 точок
Для оцінювання кластерів сформулюємо ряд ознак: розміри, координати, питома густина об’єкта, його питомий об’єм, дисперсія. Зокрема, діаметр Dk кластера – це віддаль між максимально віддаленими об’єктами k -го кластера:
(2.12)
де J – множина всіх можливих пар номерів об’єктів у k -ому кластерів.
Координати центру кластера визначаємо за наступною формулою:
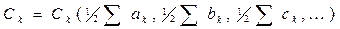. (2.13)
Інтегральною оцінкою отриманих кластерів сформулюємо як середню питому густину всіх об’єктів:
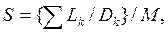(2.14)
або їй оберненою величиною питомого об’єму на один ключ:
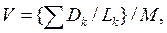(2.15)
де Lk, Dk – кількість об’єктів та діаметр k -го кластера, M – кількість отриманих кластерів.
Близьким до вказаних оцінок є критерій Варда (Ward) відхилень квадратів – функція питомої дисперсії кластерів:
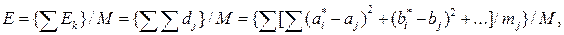(2.16)
де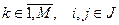 
, ai*, bi*, ci* – координати центра простору кластера,
Ek – дисперсія k -го кластера, dj – середньоквадратичне відхилення ключа від центру простору кластера, mj – кількість об’єктів у j -ому кластері.
У багатовимірному просторі з різними центрами та однаковими радіусами (як частинний випадок) критерієм якості отриманих кластерів приймаємо різницю між максимальним та мінімальними діаметрами отриманих кластерів, тобто
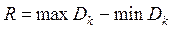. (2.17)
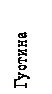
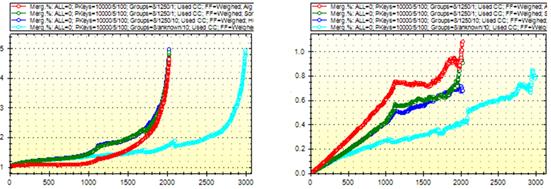
а б
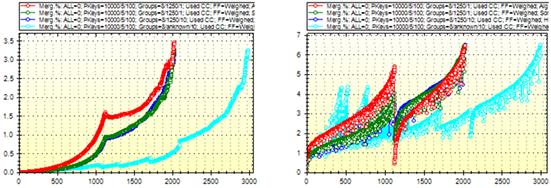
в г
Рис. 2.1. Залежності функції якості від рівня дерева згортання:
а – функція густини, б – функція об’єму,
в – функція дисперсії, г – функція сусідства
|
|