
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Базові поняття криптографії
|
|
Суть криптографії у забезпеченні конфіденційності даних (відкритого тексту, секретного ключа) шляхом їх шифрування.
Крім забезпечення конфіденційності, криптографія застосовується для розв'язання таких задач, як:
• перевірка справж ності (автентифікація). Одержувач може встановити відправника, а зловмисник не може під нього маскуватися;
• цілісність. Отримувач може перевірити несанкціоновану модифікацію в тексті, а зловмисник не може видати підробний текст за справжній;
• н е заперечення авт орства. Відправник не може в подальшому заперечувати відсилку даних.

|
| Сучасна криптографія містить у собі чотири базові розділи: • сішетрич)н криптосистеми (системи з секретним ключем або одноключові); |
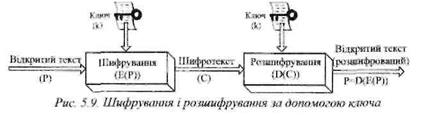
Початкове повідомлення називають відкритим текстом Р (plaintext), а процес приховування його семантичного змісту називають шифруванням і позначають Е (encipher). В результаті шифрування утворюється шифрогекст С (ciphertext), а одержання початкового відкритого тексту здійснюється в процесі розшифрування D (decipher) шифротексту (криптограми). Ця послідовність показана на рис.5-8. В математичній формі функція шифрування і розшифрування відповідно записується як Е(Р)=С і D(C)=P, а оскільки ЕЧС) є відновлення Р, то справедливо D(E(P))=P. симетричні криптографічні системи (системи з відкритим ключем або двоключові);
• криптографічні протоколи;
• керування ключами.
Криптографічний алгоритм, також: названий шифром, це математична функція, яка використовується для шифрування і розшифрування.
Якщо безпека алгоритме заснована на збереженні самого алгори-тма в таємниці, то це обмежений алгоритм. Обмежені алгоритми представляють тільки історичний інтерес, оскільки не відповідають сьогоднішнім стандартам і не допускають можливості якісного контролю чи стандартизації. Крім того, у кожної фупи користувачів повинен бути свій унікальний алгоритм і такі групи не можуть використовувати відкриті апаратні чи програмні продукти, оскільки зловмисник може купити такий самий продукт і розкрити алгоритм.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Сучасна криптографія вирішує ці проблеми за допомогою ключа К. (key), що використовується в функціях Е і D може приймати будь-яке значення і бути обраним з великої множини, яку називають простором ключів. Ключовий простір розглядаються як потужність множини ключів, які використовують для даного шифра. Тоді відносно К функції Е і D приймають вигляд Лк (Р) = С, Dk (С) = Р, при
цьому справедлива рівність Dk(Ek(PJ) = Р (див. рис.6.9).
Для деяких алгоритмів при шифруванні і розшифруванні використовуються різні ключі Кі - для шифрування, К2 - для розшифрування, то в цьому випадку Ак (Р) = С, Dkt(C) = P,
Dki (Ekt (P)) = Р (див. рис. 6.10).
Безпека цих алгоритмів цілком заснована на ключах, а не на деталях алгоритмів. Це значить, що алгоритм може бути опублікований і проаналізований. Продукти, що використовують цей алгоритм, можуть широко тиражуватися. Не має значення, що зловмисникувідомий алгоритм, якщо йому не відомий конкретний ключ, то він не зможе прочитати шифротекст.

В криптографії існують дві базові методології з використаїшям ключів - симетрична (див. рис. 5.9) і асиметрична (див. рис. 6.10) і які відповідно називають із секретним і відкритим ключем. Кожна ме-тодолоітя використовує свої власні процедури, свої способи розподілу ключів, їх типи, алгоритми шифрування і розшифрування ключів.
Для сучасних криптографічних систем захисту інформації існу ють загальні вимоги, до яких відносяться:
• шифротекст (С) повинен піддаватися читанню тільки при наявності ключа (к);
• число операцій, необхідних для визначення ключа (к) шифрування, за фрагментом шифротсксту (С) і відповідного йому відкритого тексту (Р), повинно бути не менше загального числа можливих ключів (к);
• число операцій, необхідних для розшифровування (D(Q) шляхом перебору всіх можливих k (лобова атака), повинно мати строгу нижню оцінку і виходити за межі можливостей сучасних та перспективних комп'ютерних систем та мереж;
• знання алгоритму шифрування не повинно впливати на надійність криптографічного захисту;
• незначна зміна ключа (к) повинна приводити до істотної зміни шифротексту (С);
, • структурні елементи алгоритму шифрування повинні бути незмінними;
• довжина шифрованого тексту (С) повинна бути близькою довжині відкритого тексту (Р);
• не повинно бути простих і легко встановлюваних залежностей між ключами, що використовуються в процесі шифрування (D(C)); • алгоритм повинен допускати, як програмну, так і апаратну реалізацію, при цьому зміна довжини ключа (к) не повинна вести до якісного погіршення алгоритму шифрування.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Спроба криптоаналізу називається розкриттям (зламуванням шифру, дешифруванням), за допомогою якого можна отримати Р, не маючи к. Успішно проведений криптоаналіз може визначити Р чи к, а також знайти слабкі місця в криптосистемах, що зрештою приведе до визначення відритого тексту чи ключа.
Основне припущення криптоаналізу, вперше сформульоване в дев'ятнадцятому столітті Датчманом А. Керкгофом (Dutchman A. Kerckhoffs) - безпека повинна цілком визначатися ключем, а крип-тоаналітик має повний опис алгоритму і його реалізації.
Покажемо відомі типи розкриття, які засновуються на припущенні, що криптоаналітик має всю повноту знання про використовуваний алгоритм шифрування.
1. Розкриття на основі тільки шифротексту. У криптоана-
літика є шифротексти (/V,, jV2,..., iV,) декількох відкритих текстів
(РІ, Р2,..., РІ), зашифрованих одним алгоритмом. Криптоаналітик
розкриває як можна більшу кількість криптограм (визначення Р), або ключів шифрування з метою розкриття інших шифротекстів, зашифрованих тим самим ключем (ключами). Іншими словами маючи #, =ад), N2 = Ek(P2),..., N; = Ek(P,)
можна визначити (Рі, Р2,..., Рі)тді k або алгоритм відновлення
Рміз См = Ек(Рм).
2. Розкриття на основі відкритого тексту. У криптоаналіти-
ка є доступ до шифротекстів (NV! V2,..., N.)\ їх відкритих текстів
(Р1, Р2,..., РІ). Він розкриває ключ (ключі) з метою розшифрування
інших шифротекстів, зашифрованих тим же ключем (ключами). Іншими словами маючи
P^=Ek{Ps), P2A^Ek{P2)? 2,..., Pi, Ni = Ek(Pi) можна визначити k або алгоритм відновлення РМЬ См=Ек(Рм).
3. Розкриття на основі підібраного відкритого тексту. У
криптоаналітика є шифровані і відкриті тексти декількох повідом
лень, а також можливість підібрати відкритий текст для шифруван
ня. Це надає більше варіантів ніж розкриття на основі відкритого
тексту, оскільки криптоаналі гик здійснює вибір блоків відкритого тексту, що підлягають шифруванню і це може дати більше інформації про ключ. Криптоаналітик одержує ключ (ключі), шифрування чи алгоритм, що дозволяє розкрити нові повідомлення, зашифровані тим же ключем (ключами). Іншими словами, маючи
РГД = ВД), Р2Л = Ек{Р2), -, Р; Д = ВД) та можливість вибирати (Р], Р2,..., РІ) визначається k або алгоритм знаходження
Рм\з См=Ек(Рм).
4. Розкриття на основі адаптивно підібраного відкритого тексту. Криптоаналітик може вибирати відкритий текст, що підлягає шифруванню, також уточнювати наступний вибір на базі раніше отриманих результатів шифрування. При розкритті з використанням підібраного відкритого тексту криптоаналітик бере для шифрування тільки один великий блок відкритого тексту, а при адаптивному вибирається менший блок і потім наступний, використовуючи результати першого вибору і т. д.
5- Розкриття з використанням підібраного шифротекста. Криптоаналітик для розкриття може вибирає різні шифротексти і має доступ до розшифрованих відкритих текстів. Наприклад, маючи " чорний ящик", що реалізує автоматичне розшифрування, необхідно одержати ключ. Іншими словами, маючи
#, /» - Dk{q), jv2p2 = /Л(С),.... ffa = Dk(C,)
визначаємо к. Таке розкриття зазвичай застосовується до систем з відкритим ключем, але іноді буває ефективним і для симетричних алгоритмів. (Часто розкритгя третього і п'ятого тину разом називають розкриттям на основі підібраного тексту.)
6. Розкриття на основі підібраного ключа. Криптоаналітик має деяку інформацію про зв'язок між різними ключами. Цей тип розкриття часто буває дуже практичний і відрізняеіься від всіх раніше розглянутих. Криптоаналітик вибирає зв'язок між парою невідомих ключів, за допомогою яких зашифровані дані. В варіанті з відомим відкритим текстом є відкритий і шифрований двома ключами текст, а в варіанті з підібраним - криптоаналітик вибирає відкритий текст для шифрування двома ключами.
7. Бандитський криптоаншііз. Криптоаналітик загрожує, використовує тортури чи шантажує кого-небудь, поки не знайде ключ.
Хабарництво іігоді називається розкриттям з купівлею ключа, часто є дуже вагомим способом зламування шифрів.
Базові шифри. Підстановочні і перестановочні шифри. До появи комп'ютерів криптографія складалася з алгоритмів на символьній основі, які або заміняли одні символи іншими, або реалізовували їх перестановку. Кращі алгоритми робили і заміни (підстановки) і перестановки (перемішування) з циклічними повторами.
Сучасні зміни полягають у тому, що алгоритми стали працювати з бітами, а не символами, що важливо хоча б з погляду розміру алфавіту (перехід з 26 елементів до двох). Більшісгь криптографічних алгоритмів комбінують підстановки і перестановки.
Підстановочмим називають такий шифр, у якому кожний символ відкритого тексту в гиифротексті замінюється іншим символом. Одержувач інвертує підстановку шифротекста, відновлюючи відкритий текст. У криптографії використовують чотири типи підс-тановочних шифрів (рис. 5.11).
Знаменит и й шифр Цезаря, є простим підстановочним шифром і дійсно дуже простим, тому, що алфавіт шифротекста є зміщеним, а не випадково розподіленим.
Прості підстановочні шифри легко розкриваються, оскільки шифр не ховас частоти використання різних символів у відкритому тексті і для відновлення, наприклад, англійського шифротексту, криптоаналітику необхідні тільки частоти зустрічаємості 26 англійських символів.
Однозвучні підстановочні шифр и використовувалися вже в 1401 році в герцогстві Мантуа. Вони більш складні для розкриття, хоча і не ховають усіх статистичних властивостей мови відкритого тексту. На основі розкриття з відомим відкритим текстом ці шифри зламуються тривіально, а на основі тільки шифротекста - складніше, але використовуючи комп'ютер це займе декілька секунд.
Поліграмні підстановочні шифри кодують відразу групи символів. Частинним випадком поліграмного шифру є біграмний Play-fair.
По.піалфавітні підстановочн і шифри були винайдені Ліном Бат-тістой (Lean Battista) у 1568 році. Вони використовувалися армією Сполучених Штатів у ході Громадянської війни в Америці. Шифр (квадрат) Віженера (Vigenere), який вперше опублікований у 1586 році і шифр Бофора (Beaufort) також є прикладами поліалфавітних підстановочних шифрів.
У поліалфавітних ігідстановочних шифрах використовується множина однобуквених ключів для шифрування тільки одного символу відкритого тексту. Першим ключем шифрується перший символ відкритого тексту, другим - другий символ, і так далі. Після використання всіх ключів вони повторюються циклічно. Якщо застосовується 20 однобуквених ключів, то кожна двадцята буква шифрується тим же ключем. Цей параметр називається періодом шифру. Шифри з довгим періодом складніше розкрити, чим з коротким, але використання обчислювальної техніки значно спростило цю задачу.

Шифр зі змінним ключем (іноді називаний книжковим шифром), що використовує один текст для шифрування іншого тексту і хоча період ключа дорівнює довжині тексту, він також може бути легко зламаний.
У перестановочному шифрі міняється не відкритий текст, а порядок символів. У простому колонковому перестановочному шифрі відкритий текст пишеться горизонтально на розграфленому листі фіксованої ширини, а шифротекст зчитується вертикально. Дешиф-рування є записом шифротекста вертикально на розграфленому листі фіксованої ширини і потім зчитування відкритого тексту горизонтально. Символи шифротекста ті ж самі, що й у відкритому тексті і мають приблизно ті самі частотні характеристики, що і звичайно.
Відповідно до базових методологій використання ключів є два відповідних базових типів алгоритмів: симетричні і асиметричні
Симетричні алгоритми, іноді називаються умовними алгоритмами, у яких ключ шифрування може бути розрахований за ключем дешифрування і навпаки.
У більшості симетричних алгоритмів ключі шифрування і дешифрування ті самі (див. рис. 5.9). Ці алгоритми, також називають алгоритмами ІЗ секретним ключем (передається секретним каналом) чи алгоритмами з одним ключем, вимагають, щоб відправник і одержувач погодили використовуваний ключ перед початком безпечної передачі повідомлень. Безпека симетричного алгоритму визначається ключем, знання якого дозволяє розшифрувати повідомлення. Тому, поки повідомлення є секретними, ключ повинний не розкриватися.
Симет ричн і алго ритми поділя ються н а дві категорії.
1) Алгоритми, що обробляють відкритий текст побітово (іноді побайтово) називаються потоковими чи алгоритмами з потоковими шифрами.
2) Алгоритми, що працюють з групами бітів, які складають блоки (наприклад, 64 біт) називаються блоковими чи алгоритмами з блоковими шифрами. До появи комп'ютерів алгоритми зазвичай обробляли відкритий текст посимвольно, що може розглядатися як потокове шифрування символів.
Алгоритми з відкритим ключем (асиметричні алгоритми) розроблені таким чином, що ключ, використовуваний для шифрування, відрізняється від ключа дешифрування (див. рис. 5.10). Більше того, ключ дешифрування не може бути (принаймні протягом певного інтервалу часу) розрахований за ключем шифрування. Алгоритми називаються " з відкритим ключем" тому, що ключ шифрування може бути відкритим і хто завгодно може використовувати його (отримуючи не секретним каналом) для шифрування відкритого тексту, але тільки власник відповідного ключа дешифрування може розшифрувати повідомлення. У цих системах ключ шифрування часто називається відкритим, а розшифрування - закритим.
Безпека алгоритмів. Різні алгоритми надають різні ступені безпеки в залежності від того, наскільки важко зламати алгоритм. Якщо вартість злому алгоритму вище, ніж варгість зашифрованих даних, то ці дані швидше за все, у безпеці. Якщо час злому алгоритму більше, ніж час, протягом якого зашифровані дані повинні зберігатися в секреті, то також, швидше за все інформація у безпеці. Якщо обсяг даних, зашифрованим одним ключем, метис, ніж обсяг даних, необхідний для злому алгоритму, і тоді, швидше за все, інформація у безпеці.
Криптографія більше цікавиться криптосистемами, що важко зламати обчислювальним способом.
Криптосистема це алгоритм плюс усі можливі відкриті тексти, шифротексти і ключі. Алгоритм вважається обчислювально безпечним (чи, як іноді називають, криптостійкими). якщо він не може бути зламаний з використаннях! доступних ресурсів зараз чи у майбутньому.
Термін " доступні ресурси" є досить розпливчастим. Складність роз криття можна визначити різними способами (див, рис. 6.12).

_.— —— .f -t ------------------------ -------- Ґ^ — г.
Як емпіричний метод складність розкриття визначається за максимальним з цих трьох коефіцієнтів. Ряд операцій розкриття припускають взаємозв'язок коефіцієнтів, наприклад, більш швидке розкриття можливе за рахунок збільшення вимог до пам'яті.
Складність виражається порядком величини. Якщо складність обробки для даного алгоритму складає 2128, то 2і' операцій погрібно для розкриття алгоритму (ці операції можуть бути складними і тривалими). Так, якщо передбачається, що обчислювальні потужності здатні виконувати мільйон операцій у секунду, і для рішення задачі використовується мільйон паралельних процесорів, одержання клю-ча займе у понад 10 років, що в мільярд раз перевищує час існування всесвіту. У той час, як складність розкриття залишається постійною (поки будь-який криптоаналітик не придумає кращого способу розкриття), потужність комп'ютерів зростає. За останні піввіку обчислювальні потужності феноменально виросли і немас ніяких причин підозрювати, що ця тенденція не буде продовжена. Багато криптографічних зломів придатні для паралельних комп'ютерів. Задача розбивається на мільярди маленьких шматочків, рішення яких не вимагає міжпроцесорної взаємодії. Оголошення алгоритму безпечним просто тому, що його нелегко зламати, використовуючи су-часігу техніку, у кращому випадку ненадійно. Якісні криптосистеми проекгуються стійкими до злому з урахуванням розвитку обчислювальних засобів на багато років вперед.
Криптографічні протоколи. Криптографія вирішує проблеми секретності, перевірки дійсності, цілісності і людської нечеспості. Можна вивчити все про криптографічні алгоритми і методи, але вони представляють тільки академічний інтерес, якщо не використовуються для вирішення будь-якої проблеми. Саме тому протоколи являються невід'ємною частиною криптографічних систем.
Протокол — це порядок дій, що починаються двома чи більше сторонами та призначений для вирішення певної задачі. " Порядок дій" означає, що протокол виконується у певній послідовності від початку до кінця, а кожна дія має свою чергу і ініціюється після закінчення попередньої. " Починаються двома чи більш сторонами" означає, що для реалізації протоколу потрібно принаймні дві особи, тому, що одна особа не зможе реалізувати протокол.
Окрема особа може виконати деякі дії, вирішуючи певну задачу (наприклад, запису на дискету), але це не протокол. Нарешті, " призначений для вирішення певної задачі" означає, що протокол повинен приводити до якогось результату. У протоколів є також і інші характеристики (див. рис. 6.13).
Виконання протоколу реалізуються діями, лінійно, поки не буде команди перейти до наступної дії, кожна з яких за меншою мірою містить в собі:
• обчислення, що виконуються однієї чи декількома сторонами;
• або повідомлення, якими обмінюються сторони.

Передача інформації і використанням симетричної криптографії.
У якісній кринтосистемі безпека цілком залежить від знання ключа й абсолютно не залежить від знання алгоритму і тому керування ключами так важливо в криптографії. Ключ повинний залишатися в секреті перед, після і протягом роботи протоколу - доти, поки повинний залишатися в таємниці переданий шифротекст, у противному випадку він відразу буде розкритий.
Симетричні криптосистеми мають наступні недоліки:
• Розподіл ключів повинен проводитися в секреті. Ключі настільки ж важливі, як і всі шифротексти, зашифровані цими ключами, тому що знання ключа дозволяє розкрити криптограми. Розподіл ключів є серйозною задачею і часто кур'єри особисто доставляють ключі за призначенням.
• Якщо ключ скомігрометований (украдений, розгаданий, випитаний, отриманий за хабар і т. ін.), то можна розшифрувати всі криптограми, зашифровані цим ключем.
• Якщо кожна пара користувачів мережі використовує окремий ключ, то загальна їх кількість швидко росте із зростанням числа користувачів. Розв'язання цієї проблеми можливе шляхом зменшення кількості користувачів, але це не завжди можливо.
Поняття однонаправленої функції є центральним у криптографії з відкритими ключами. Односпрямовані {однонаправлені) функції відносно легко обчислюються, але інвертуються досить складно.Хорошим прикладом такої функції може бути розбита на тисячу малесеньких шматочків ваза, яку нелегко знову скласти з цих шматочків.
Строгого математичного доказу існування однонаправлених функцій немає, як немає і реальних свідчень можливості їхньої побудови. Незважаючи на це, багато функцій виглядають у точності як од-носнрямовані і їх можна розрахувати, але дотепер, не має простого способу інвертувати їх. Наприклад, в обмеженій області легко обчи-
слити х, але набагато складніше X х
Однонаправлена функція з секретом (функція-пастка) - це особливий тип однонаправленої функції із секретним люком. ЇЇ легко обчислити в одному напрямку і важко - у зворотному. Але якщо вам відомий секрет, ви можете легко розрахувати і зворотну функцію. Тобто, легко обчислити f(xj за відомим х, але важко за відомою f(x) обчислити х. Однак, існує невелика секретна інформація, у, що дозволяє, при знанні f(x) і у, легко обчислити х.
Вагомим прикладом однонаправленої функції з секретом може бути годинник, який легко розібрати на сотні маленьких деталей і важко знову зібрати. Але, із секретною інформацією (інструкцією зі збирання) набагато легше вирішити цю задачу.
У однонаправленої хеш-функції може бути низка імен: функція стискання, функція згортки, дайджест повідомлення, цифровий відбиток, характерна ознака, криптографічна контрольна сума, код цілісності повідомлення, код виявлення маніпуляцій та ін. Але як би не називалась ця функція вона є центральною в сучасній криптографії і особливо важливе значення має при реалізації багатьох протоколів.
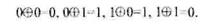
|
| Суть хеш-функції полягає в одержанні цифрового відбитку прообразу, тобто утворення значення, за яким можна встановити іденти- |
Хеш-функції, які довгий час використовувалися в комп'ютерних науках є математичними чи іншими функціями, які одержують на вході рядок змінної довжини (прообраз) і перетворюють його в рядок фіксованої, зазвичай меншої, довжини (значення хеш-функції, згортка). Приклад такої згортки може бути реалізовано за допомогою бінарної функції XOR шляхом одержання прообразу і повертання байта, утвореного виконанням операції побітового складання за модулем 2 (®) всіх бітів вхідних байтів, дечність отриманого прообразу і дійсного. Оскільки хеш-функція є співвідношенням " багато до одного", то неможливо з усією визначеністю сказати, що два цифрові відбитки різних документів не збігаються, але хеш-функцію можна використовувати, для оцінки з прийнятною точністю.
Однонаправлена хеш-функція - це хеш-функція, що працює тільки в одному напрямку, тобто легко обчислити її значення за прообразом, але важко створити прообраз, значення хеш-функції якого дорівнює заданій величині. Зазначимо, що якісні односпрямовані хеш-функції це хеш-функція без колізій (зіткнень), тобто достатньо важко створити два прообрази з однаковим значенням хеш-функції.
Хеш-функція є відкритою і секрету її розрахунку не існує. Безпека однонаправленої хеш-функції полягає саме в її однонаправленос-ті. Зміна одного біта прообразу приводь до зміни, у середньому, половини бітів значення хеш-функції. Обчислювально неможливо знайти прообраз, що відповідає заданому значенню хеш-функції.
Код перевірки дійсності повідомлення (message authentication code, MAC), відомий також як код перевірки дійсності даних (data authentication code, DAG), є однонаправленою хеш-функцією з додаванням секретного ключа. Тоді значення хеш-функції залежить від і прообразу і ключа. У цьому випадку теорія залишається тією самою, що і для хеш-функцій, але тільки той, хто знає ключ, може перевірити значення функції.
Організація зв'язку з використанням асиметричної криптографії.
У 1976 році Уітфілд Діффі і Мартін Хеллман змінили парадигму криптографії (яка засновувалась на одноключових системах), описавши асиметричну криптографію, що базується на двох різних ключах - відкритому і закритому. Визначення закритого ключа за відкритим вимагає величезних обчислювальних ресурсів. Хто завгодно, використовуючи відкритий ключ може зашифрувати повідомлення, але не розшифрувати його. Розшифрувати шифротекст може тільки власник закритого ключа. Це схоже на поштову скриньку, де процес шифрування з відкритим ключем можна порівняти з опусканням у її проріз листа, що може зробити кожний. Розшифрування закритим ключем нагадує витягування листа з поштової скриньки, що набагато складніше і може знадобитися зварювальний агрегат, але якщо знати секрет (код замка від поштової скриньки), можна легко дістати лист.
Математичною основою процесу є односпрямовані хеш-функції з секретом, за допомогою яких легко реалізується шифрування в прямому напрямку, а дешифрування - в зворотному і воно настільки важке, що, не знаючи секрету, навіть на комп'ютерах Cray за тисячі (і мільйони) років неможливо розшифрувати криптограму. Секретом (люком) служить закритий ключ, який робить розшифрування таке ж простим, як і шифрування.
Слід зазначити, що криптографія з відкритими ключами усуває проблему розподілу ключів, властиву симетричним криптосистемам.
Зазвичай ціла мережа користувачів приймає для використання певну асиметричігу криптосистему. У кожного з них є відкритий і закритий ключ, при цьому відкриті ключі містяться в загальнодоступній базі даних. Ось як на основі цієї криптографії відправник може переправити повідомлення одержувачу:
1. Відправник і одержувач домовляються використовувати асиметричну криптосистему.
2. Одержувач посилає відправнику свій відкритий ключ.
3. Відправник шифрує своє повідомлення, використовуючи відкритий ключ одержувача і відсилає його.
4. Одержувач приймає і розшифровує повідомлення своїм секретним ключем.
Змішані (гібридні) криптосистеми. Алгоритми з відкритими ключами не заміняють симетричні алгоритми і використовуються не для шифрування повідомлень, а для шифрування ключів за наступними двома причинами:
1. Алгоритми з відкритими ключами працюють повільно. Симетричні алгоритми принаймні в 1000 разів швидше, ніж алгоритми з відкритими ключами. Так, комп'ютери стають усе швидше і швидше і років через 15 криптографія з відкритими ключами досягне швидкостей, порівнянних із сьогоднішньою швидкістю симетричної криптографії. Але вимоги до обсягу переданої інформації також зростають, і завжди буде вимагатися шифрувати дані швидше, ніж це зможе зробити криптографія з відкритими ключами.
2. Криптосистеми з відкритими ключами уразливі стосовно розкриття на основі підібраного відкритого тексту. Криптоаналітик не зможе розкрити к, але зможе визначити Р.
Розкриття на основі підібраного відкритого тексту може бути особливо ефективним, якщо число можливих шифротекстів відносно мале. Наприклад, якщо Р - це грошова сума в доларах, менша ніж
$1000000, то таке розкриття спрацює, криптоаналітик перебере весь мільйон значень. Навіть якщо Р не так добре визначене, таке розкриття може бути дуже ефективним. Корисним може бути також просте знання того, що шифротекст не відповідає конкретному відкритому тексту. Симетричні криптосистеми не чуттєві до розкрипів такого типу, тому що криптоаналітик не може виконати тестових розшифрувань з невідомим ключем.
У більшості реалізацій криптографія з відкритими ключами використовується для засекречування і розповсюдження сеансових ключів, що використовуються симетричними алгоритмами для закриття потоку повідомлень. Іноді такі реалізації називаються змішаними (гібридними) криптосистемами.
Використання криптографії з відкритим ключем для розподілу секретних ключів вирішує дуже важливу проблему їх розподілу.
|
|
