
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Законы движения космических тел
|
|
Законы Кеплера формулируются в предельно упрощенной форме:
I. Все планеты Солнечной системы вращаются вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце.
II. Радиус-вектор планеты за одинаковые промежутки времени описывает равные площади: скорость движения планет максимальна в перигелии и минимальна в афелии.
III. Квадраты периодов обращения планет вокруг Солнца соотносятся между собой, как кубы их средних расстояний от Солнца:
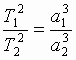
Упрощенный вывод закона Всемирного тяготения описан в учебнике физики для физико-математических школ под редакцией А.А. Пинского [49, с. 22]:
Если планеты движутся по почти круговым орбитам, их центростремительные ускорения равны:
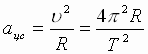 (1),
(1),
где Т – период обращения планеты вокруг Солнца, R - радиус орбиты планеты.
Из III закона Кеплера
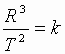 или
или 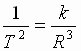 (2).
(2).
Следовательно, ускорение любой планеты независимо от ее массы обратно пропорцио-нально квадрату радиуса ее орбиты:
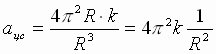 (3)
(3)
Согласно II закону Ньютона, сила F, сообщающая планете это ускорение, равна:
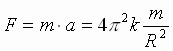 (4)
(4)
сила, действующая на любую планету, прямо пропорциональна массе планеты и обратно пропорциональна квадрату расстояния от нее до Солнца.
Согласно III закону Ньютона, сила F¢, действующая на планету со стороны Солнца, равна ей по модулю, противоположна по направлению и равна:
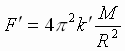 (5,
(5,
где М – масса Солнца.
Поскольку F = F¢,
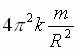 =
= 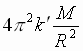 .
.
Обозначим  где G – постоянная величина. (6)
где G – постоянная величина. (6)
Тогда
 (7)
(7)
и выражение (4) можно записать в виде известной нам формулы закона Всемирного тяготения:
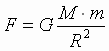 (8):
(8):
Сила тяготения между Солнцем и планетой пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
1. Изложение истории открытия законов Кеплера и закона Всемирного тяготения. Определение законов Кеплера и закона Всемирного тяготения.
2. Вывод законов Кеплера на основе закона Всемирного тяготения и законов механики.
| 
|
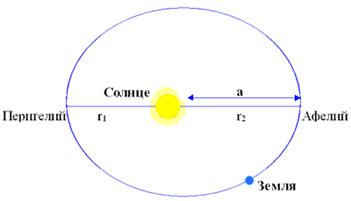
| Рис. 58 Законы Кеплера | Рис.59 Второй закон Кеплера |
А.И. Фетисов предлагает качественный вывод I и II законов Кеплера, повторяющий рассуждения автора открытия:
Кеплеру были известны: координаты планеты (Марса) на небесной сфере с точностью до 2¢ по данным наблюдений Т. Браге; относительные расстояния планет от Солнца; синодические и сидерические периоды обращения планет.
Далее он мог рассуждать:
|
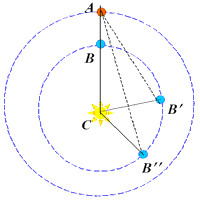
| Рис. 60 |
Известно положение Марса во время противостояния (рис. 60). В треугольнике АВС буква А обозначает положение Марса, В - Земли, С – Солнца. Через промежуток времени, равный сидерическому периоду обращения Марса (687d) планета вернется в точку М, а Земля за это время переместится в точку В¢. Поскольку угловые скорости движения Земли в течение года известны (они равны угловым скоростям видимого движения Солнца по эклиптике), можно вычислить угол АСВ¢. Определив координаты Марса и Солнца в момент прохождения Землей через точку В¢, мы можем, зная в треугольнике 2 угла, по теореме синусов рассчитать отношение стороны СВ¢ к АС. Еще через один оборот Марса Земля придет в положение В" и можно будет определить отношение СВ" к тому же отрезку АС и т.д. Таким образом, точка за точкой можно получить представление об истинной форме орбиты Земли, установит, что она является эллипсом, в фокусе которого находится Солнце (I закон Кеплера); что в ближайшей к Солнцу точке своей орбиты Земля движется наиболее быстро, а в самой далекой – наиболее медленно (II закон Кеплера).
Более сложный (но и более подробный, количественный) вывод законов Кеплера можно осуществить согласно методике Ю.И. Соколовского [271]. Изложение материала удобнее начинать с вывода II закона Кеплера как наглядно-геометрического истолкования закона сохранения момента импульса.
Сила гравитационного притяжения планеты Солнцем направлена к ее центру, ее момент относительно любой оси, проходящей через центр, равен нулю. Момент импульса планеты N остается неизменным:
N = m× u ^ × r = m× u × h = const, где m – масса планеты, r – расстояние от Солнца, u - скорость планеты; u ^ - составляющая этой скорости, перпендикулярная направлению на Солнце; h – длина перпендикуляра, опущенного из центра Солнца на вектор скорости или его продолжение. При неизменной массе планеты из сохранения момента импульса следует постоянство произведения момента скорости u × h: u × h = N/m = const. Пусть u × h = n.
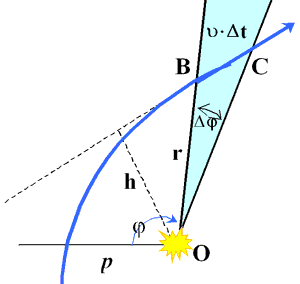
|
| Рис. 61 |
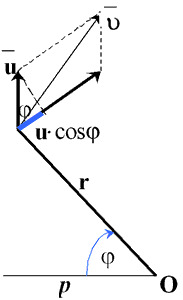
За промежуток времени D t планета перемещается вдоль орбиты на расстояние ВС = u × D t. Радиус-вектор ОВ как бы " ометает" сектор орбиты ВОС – треугольник с несколько искривленным основанием ВС = u × D t и высотой h. Его площадь: 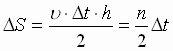 . Следовательно, отношение
. Следовательно, отношение 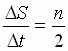 для данной орбиты постоянно. Оно характеризует быстроту " ометания" площади, численно равно площади сектора, " ометаемого" радиус-вектором за единицу времени и называется секторальной скоростью (рис. 61).
для данной орбиты постоянно. Оно характеризует быстроту " ометания" площади, численно равно площади сектора, " ометаемого" радиус-вектором за единицу времени и называется секторальной скоростью (рис. 61).
Для вычисления площади S, " ометаемой" за промежуток времени t, разобьем его на элементарные промежутки D t1, D t2, D t3 … Тогда: 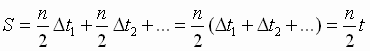 , откуда следует формулировка II закона Кеплера: " За любые равные промежутки времени радиус-вектор планеты " ометает" равные площади ".
, откуда следует формулировка II закона Кеплера: " За любые равные промежутки времени радиус-вектор планеты " ометает" равные площади ".
Ученикам напоминают определение эллипса и способ его практического построения.
Эллипс - кривая II порядка, для любой точки которой сумма расстояний от двух точек, называемых фокусами эллипса, постоянна (рис. 58). Степень вытянутости эллипса характеризуется эксцентриситетом е, 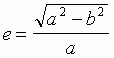 , где a и b - полуоси эллиптической орбиты. При совпадении фокусов с центром (е = 0) эллипс превращается в окружность; при е = 1 становится параболой; при е > 1 - гиперболой.
, где a и b - полуоси эллиптической орбиты. При совпадении фокусов с центром (е = 0) эллипс превращается в окружность; при е = 1 становится параболой; при е > 1 - гиперболой.
Вывод I закона Кеплера: Движение планет удобно описывать в полярной системе координат, начало которой О совмещено с Солнцем: положение планеты определяется полярным расстоянием r и полярным углом j (рис. 58). Рассмотрим орбиты с одинаковыми моментом скорости n и секторальной скоростью 0, 5 n. При движении по любой из них планета пересечет сектор ВОС с углом D j при вершине и площадью D S = 0, 5 r2× D j за время: 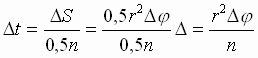 (1) Ускорение планеты а ц определяется притяжением Солнца; по закону Всемирного тяготения:
(1) Ускорение планеты а ц определяется притяжением Солнца; по закону Всемирного тяготения: 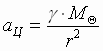 (2). Из (1), (2) определяется модуль изменения вектора скорости планеты за время пересечения рассматриваемого сектора:
(2). Из (1), (2) определяется модуль изменения вектора скорости планеты за время пересечения рассматриваемого сектора: 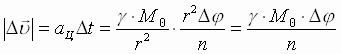 . Модуль изменения вектора скорости определяется моментом скорости n и углом D j при вершине сектора и не зависит от расстояния планеты от Солнца, т.к. ослабление гравитации с удалением от Солнца компенсируется увеличением длительности ее воздействия.
. Модуль изменения вектора скорости определяется моментом скорости n и углом D j при вершине сектора и не зависит от расстояния планеты от Солнца, т.к. ослабление гравитации с удалением от Солнца компенсируется увеличением длительности ее воздействия.
Пусть радиус круговой орбиты r к, а модуль линейной скорости планеты u к. Вектор этой скорости меняется при движении только по направлению, оставаясь перпендикулярным радиусу, так что момент скорости n = r кuк. Радиус круговой орбиты определяется, отождествляя ускорение планеты с центростремительным ускорением: 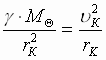 , но
, но 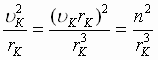 (3) Þ
(3) Þ 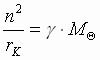 (4) и
(4) и 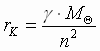 . При движении планеты с тем же моментом скорости по любой другой орбите вектор ее линейной скорости будет иным, но изменяться при прохождении сектора с углом D j будет на ту же величину D` u, что и при движении по окружности. Значит, векторы ` u и ` u кмогут отличаться друг от друга только на постоянное по модулю и по направлению векторное слагаемое u: ` u =` u к +` u. Направим полярную ось ОР перпендикулярно вектору u так, чтобы в точке Р векторы` u к и` u совпадали по направлению. В произвольном положении планеты ее линейная скорость` u геометрически складывается из скорости` u к и постоянного вектора` u. Момент скорости равен сумме моментов ее составляющих: n = r× u к + r× u× cosj Þ
. При движении планеты с тем же моментом скорости по любой другой орбите вектор ее линейной скорости будет иным, но изменяться при прохождении сектора с углом D j будет на ту же величину D` u, что и при движении по окружности. Значит, векторы ` u и ` u кмогут отличаться друг от друга только на постоянное по модулю и по направлению векторное слагаемое u: ` u =` u к +` u. Направим полярную ось ОР перпендикулярно вектору u так, чтобы в точке Р векторы` u к и` u совпадали по направлению. В произвольном положении планеты ее линейная скорость` u геометрически складывается из скорости` u к и постоянного вектора` u. Момент скорости равен сумме моментов ее составляющих: n = r× u к + r× u× cosj Þ
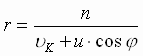 или
или 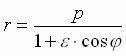 (5), где
(5), где 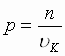 и
и 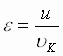 – постоянные величины.
– постоянные величины.
Выражение (5) полностью определяет форму орбиты. При e < 1 оно представляет собой уравнение эллипса с фокальным параметром р и эксцентриситетом e, один из фокусов которого совпадает с центром координат – центром Солнца. При e = 1 уравнение (5) описывает параболу; при e > 1 – гиперболу. Формулируем I закона Кеплера: " Планетные тела движутся по орбитам, представляющим собой кривые II порядка, в одном из фокусов которых находится центр масс системы ".
При j = 0 расстояние планеты от Солнца минимально и равно 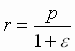 ; в этой точке перигелия скорость планеты максимальна и равна` u к +` u. При j = p, в афелии, модуль скорости имеет минимальное значение` u к -` u. При j = ± p /2 расстояние от Солнца равно р, чем раскрывается геометрический смысл фокального параметра. При e = 0 расстояние от Солнца равно р при любом j, т.е. планета движется по окружности. Это имеет место и при u = 0, т.е. при начальной и неизменной по модулю скорости планеты u = u к + u = u к. Т.о. параметр р есть радиус круговой орбиты с данным моментом импульса, а скорость u к – круговая или I космическая скорость на расстоянии r к = р от Солнца.
; в этой точке перигелия скорость планеты максимальна и равна` u к +` u. При j = p, в афелии, модуль скорости имеет минимальное значение` u к -` u. При j = ± p /2 расстояние от Солнца равно р, чем раскрывается геометрический смысл фокального параметра. При e = 0 расстояние от Солнца равно р при любом j, т.е. планета движется по окружности. Это имеет место и при u = 0, т.е. при начальной и неизменной по модулю скорости планеты u = u к + u = u к. Т.о. параметр р есть радиус круговой орбиты с данным моментом импульса, а скорость u к – круговая или I космическая скорость на расстоянии r к = р от Солнца.
|
| Рис.62 |
Орбита имеет параболическую форму при e = 1, u = u к. В соответствие с (5) при e = 1 и j = 0 перигелий параболической орбиты находится на расстоянии р /2 от Солнца. Чтобы тело двигалось по параболе, надо сообщить ему в перигелии начальную скорость: u = u к + u = u к + u к = 2u к – параболическую или II космическую. Круговая (I космическая) скорость в этой точке равна 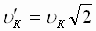 . Т. к. через u к была обозначена круговая скорость для вдвое большего удаления от Солнца r к = p, а по (4) значение круговой скорости обратно пропорционально
. Т. к. через u к была обозначена круговая скорость для вдвое большего удаления от Солнца r к = p, а по (4) значение круговой скорости обратно пропорционально 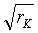 , параболическая u П скорость равна
, параболическая u П скорость равна 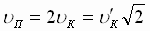 , т.е. в
, т.е. в 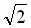 раз превышает круговую для той же точки.
раз превышает круговую для той же точки.
Вывод III закона Кеплера: Благодаря постоянству секторальной скорости период обращения планеты Т определяется делением " ометаемой" за 1 оборот площади эллипса S на секторальную скорость n /2. Т.к. площадь эллипса S = p × a× b, где a и b – большая и малая полуоси.
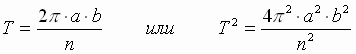 (6). Т.к. для эллипса b 2 = p× a,
(6). Т.к. для эллипса b 2 = p× a, 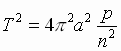 (7). Учитывая, что p = r к и (4), получим
(7). Учитывая, что p = r к и (4), получим 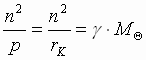 . Тогда формула (7) запишется:
. Тогда формула (7) запишется: 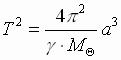 .
.
В этом выражении 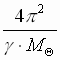 – величина постоянная (
– величина постоянная ( одинакова для всех планет Солнечной системы), поэтому для любых двух ее планет:
одинакова для всех планет Солнечной системы), поэтому для любых двух ее планет: 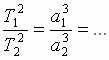 Формулируем III закон Кеплера: " Квадраты периодов обращения двух планет соотносятся как кубы больших полуосей их орбит ".
Формулируем III закон Кеплера: " Квадраты периодов обращения двух планет соотносятся как кубы больших полуосей их орбит ".
В пособии [167? ] предлагается следующий вывод уточненного III закона Кеплера для кругового движения:
Согласно закону Всемирного тяготения, ускорения двух взаимно притягивающихся и обращающихся вокруг общего центра масс космических тел равны: 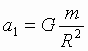 ,
,  (1), где M и m – массы тел, R - расстояние между их центрами.
(1), где M и m – массы тел, R - расстояние между их центрами.
Угловая скорость их обращения вокруг центра масс равна 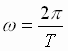 , где Т – период обращения. Тогда центростремительное ускорение тел:
, где Т – период обращения. Тогда центростремительное ускорение тел: 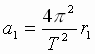 ,
, 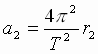 (2), где r 1 и r 2 - расстояния тел от центра масс системы.
(2), где r 1 и r 2 - расстояния тел от центра масс системы.
Приравнивая выражения (1) и (2), получим: 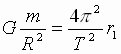 ,
, 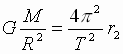 (3).
(3).
Складывая почленно выражения (3), получим: 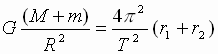 Þ
Þ 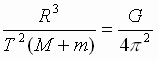 (4).
(4).
В правой части выражения (4) находятся лишь постоянные величины, откуда следует его справедливость для любой системы двух гравитационно взаимодействующих тел. Для двух космических систем это выражение запишется в виде уточненного III закона Кеплера:
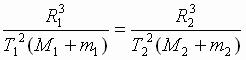 Þ
Þ 
3. Полная формулировка законов движения космических тел в центральном поле тяготения и определение понятий, связанных с описанием движения космических тел и характеристиками орбит:

|
| Рис. 63. Элементы орбит |
Основные характеристики движения космического тела в пределах Солнечной системы – называются элементами орбиты и определяются относительно плоскости эклиптики (рис. 63).
Угол i между плоскостью орбиты и эклиптикой называется ее наклонением: при 0њ £ i < 90њ космическое тело движется вокруг Солнца в прямом направлении (как Земля); при 90њ £ i < 180њ – в обратном направлении.
Точки, в которых орбита космического тела пересекается с плоскостью эклиптики, называются узлами егоорбиты: восходящим узлом в направлении северного полюса эклиптики и нисходящим узлом в направлении южного полюса эклиптики.
Угол b между центром Солнца, восходящим узлом орбиты и точкой весеннего равноденствия называется гелиоцентрической долготой восходящего узла и вместе с наклонением определяет пространственное положение плоскости орбиты космического тела.
Угол w между центром Солнца, восходящим узлом орбиты и точку перигелия называется угловым расстоянием перигелия от узла, отсчитывается в плоскости орбиты в направлении движения космического тела и определяет положение орбиты в ее плоскости.
Момент прохождения перигелия t 0 определяет положение космического тела на орбите в данное время.
Большая полуось орбиты а является средним расстоянием космического тела от Солнца и определяет размеры его орбиты: 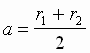 ,
, 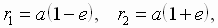 где r 1 - расстояние космического тела от Солнца в перигелии, r 2 - в афелии.
где r 1 - расстояние космического тела от Солнца в перигелии, r 2 - в афелии.
Большая полуось земной орбиты принята за астрономическую единицу расстояний: аÅ = 1 а. е. = 149000000000 м.
Определением положений объектов Солнечной системы на небесной сфере по элементам их орбит (вычислением эфемерид космических тел) и определением элементов орбит космических тел на основе наблюдений их видимого движения занимается теоретическая астрономия.
Для определения характеристик орбиты космического тела необходимо провести не менее 3 измерений экваториальных координат светила на небесной сфере (точность вычислений повышается при увеличении количества наблюдений). На основе данных наблюдений составляется система из 6 уравнений, каждое из которых содержит известные экваториальные координаты светила и в качестве неизвестной величины – один из элементов орбиты космического тела. Классический способ решения задачи был метод " наименьших квадратов"; в настоящее время для расчетов широко применяются ЭВМ.
I закон Кеплера:
Траектории движения небесных тел в центральном поле тяготения представляют собой коническое сечение (кривую II порядка): эллипс, окружность, параболу или гиперболу, в одном из фокусов которой находится центр масс системы.
орбиты планет Солнечной системы имеют форму эллипса, в одном из фокусов которого находится Солнце. Масса Солнца в 750 раз больше массы всех остальных тел Солнечной системы, поэтому центр масс Солнечной системы находится внутри Солнца, почти совпадая с его геометрическим центром. Эллиптические орбиты имеют спутники планет, в том числе ИСЗ, астероиды и часть комет. Эксцентриситет е планетных орбит очень мал (еÅ = 0, 017). Эксцентриситеты орбит астероидов значительно больше, многие кометы имеют параболические и гиперболические орбиты.
Перицентром называется ближайшая к центру масс системы точка орбиты небесного тела; апоцентром - наиболее удаленная. Для орбит небесных тел, вращающихся вокруг Солнца, они будут соответственно называться перигелием и афелием; для орбит тел, вращающихся вокруг Земли - перигеем и апогеем и т. д.
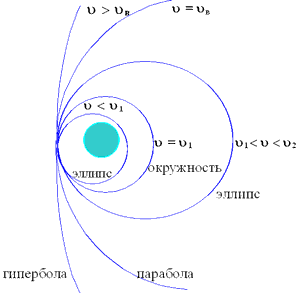
|
| Рис.64 Космические скорости. Зависимость формы орбиты от скорости небесного тела |
Орбита небесного тела зависит от его скорости в данной точке пространства (рис. 64).
I космическая скорость является скоростью кругового движения: 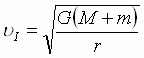 .
.
Для ИСЗ, запускаемых на околоземные низкие орбиты (h = 200 км), u I =7, 78 км/с.
II космическая скорость - скорость параболического движения: 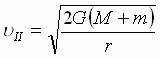 .
.
Для стартующих с Земли автоматических межпланетных станций u II = 11, 02 км/с.
При u I < u < u II тело движется по эллиптической орбите. При u < u I тело также движется по эллиптической орбите, которая за исключением точки апоцентра будет целиком лежать внутри круговой орбиты. Такие траектории полета земных космических летательных аппаратов (КЛА) называются баллистическими. Период вращения небесных тел вокруг центра масс можно определить по формуле: 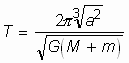 .
.
При u > u II траектория движения небесного тела представляет собой гиперболу.
Скорость, с которой запущенный с Земли КЛА покинет пределы Солнечной системы, называют иногда третьей космической скоростью. Она равна сумме скоростей движения Земли вокруг Солнца и II космической скорости КЛА относительно Земли, u III = 42 км/с.
II закон Кеплера:
Прямая, соединяющая небесное тело с центром масс, описывает равные площади в равные промежутки времени, то есть площадь, описанная радиус-вектором тела, пропорциональна времени, в течение которого она описана: при t 1 = t 2, S 1 = S 2, u 1¹ u 2 (u 1> u 2) (рис. 59)
Так как за одно и то же время небесное тело проходит разные по протяженности участки орбиты, его движение будет неравномерным. Небесные тела вблизи перицентра имеют скорость большую, чем вблизи апоцентра: 
III закон Кеплера:
Произведение сумм масс небесных тел и их спутников с квадратами их сидерических периодов обращение относятся как кубы больших полуосей их орбит:
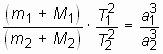 , где М 1 и М 2 - массы небесных тел, m 1 и m 2 - соответственно массы их спутников, а 1 и а 2 - большие полуоси их орбит, Т 1 и Т 2 - сидерические периоды обращения.
, где М 1 и М 2 - массы небесных тел, m 1 и m 2 - соответственно массы их спутников, а 1 и а 2 - большие полуоси их орбит, Т 1 и Т 2 - сидерические периоды обращения.
Ученики должны понять, что закон Кеплера связывает характеристики движения компонентов любых произвольных и независимых космические систем.
Изученный материал закрепляется в ходе решения задач.
Упражнение 7:
1. К Земле или к Солнцу сильнее притягиваются: а) ИСЗ; б) Луна [Ответ: FТ¤ » 2, 5FТÅ ].
2. Почему Солнце не может оторвать Луну от Земли?
3. Задача из статьи В.Б. Дроздова [55]: Какова должна быть минимальная скорость жюль-верновского снаряда, чтобы он попал в Луну? Какую скорость он будет иметь у ее поверхности? [Ответ: 11, 1 км/с; 2, 3 км/с].
4. Какова продолжительность сидерического периода вращения Юпитера вокруг Солнца, если он в 5 раз дальше от Солнца, нежели Земля? Через какие промежутки времени повторяются его противостояния?
5. Определите периоды обращения ИСЗ, двигающихся по орбитам 1, 2 и 3 вокруг Земли на рис. 64. Радиус Земли 6370 км.
6. Какую скорость должна иметь на старте с поверхности Луны (Марса) ракета, доставляющая на Землю образцы грунта?
| < < Предыдущая | Содержание | Следующая > > |
| Публикации с ключевыми словами: методика преподавания - преподавание астрономии - наблюдения - лабораторные работы - практические работы - учебная программа - учебные пособия - лекции - педагогический эксперимент - дидактика - контрольные работы - задача Публикации со словами: методика преподавания - преподавание астрономии - наблюдения - лабораторные работы - практические работы - учебная программа - учебные пособия - лекции - педагогический эксперимент - дидактика - контрольные работы - задача | |
См. также:
 Иллюзия одинаковых цветов Иллюзия одинаковых цветов
 Лекторий Планетария открывает двери Лекторий Планетария открывает двери
 Syfy Poehali Party в Политехническом музее Syfy Poehali Party в Политехническом музее
 Исследование кометы 2010 года по наблюдениям с космической орбитальной обсерватории SOHO. Исследование кометы 2010 года по наблюдениям с космической орбитальной обсерватории SOHO.
 Студенческая астрономическая обсерватория ГАИШ Студенческая астрономическая обсерватория ГАИШ
 Куда сообщать о " летающих тарелках"? Новый проект в рамках МГА2009. Куда сообщать о " летающих тарелках"? Новый проект в рамках МГА2009.
 Летнее небо Астрономического города Летнее небо Астрономического города
|
|
|
