Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Березенцева Т.Н.

Негосударственное образовательное учреждение высшего профессионального образования

«РОССИЙСКИЙ НОВЫЙ УНИВЕРСИТЕТ»

Воскресенский филиал

Кафедра прикладной информатики и естественнонаучных дисциплин

Контрольная работа

По теории алгоритмов

IV-вариант

Выполнил:

студента 2 курса на базе среднего профессионального (профильного) образования заочной формы обучения группы ИП11 Макарова Юрий Игоревич

Проверил:

старший преподаватель

Березенцева Т.Н.

Воскресенск

2013 г.

1. Определить, какая функция получается при суперпозиции функции g(x)=x+1 с самой собой.

h(x)= g(g(х))=x+2

Ответ: Суперпозиция функции g(х) с самой собой получим функцию h(х) = х + 2.

2. Определить, какая функция возникает примитивной рекурсией из функций g= x и h=x^z.

f(0)=g(0)=0;

f(1)=h(0, g(0))=0⁰=0;

f(2)=h(1, f(1))=1⁰=1;

f(3)=h(2, f(2))=2¹=2;

f(4)=h(3, f(3))=3²=9;

…

f(x)=(x-1)^(x-2)

Ответ: Примитивная рекурсией из функций g= x и h=x^z есть функция f(x)=(x-1)^(x-2)

3. Покажите, что функция f(x, y)= 2x+3y является примитивно рекурсивной.

Доказательство.

Функция f(x; y) удовлетворяет соотношениям: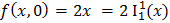

f(x; y + 1) =2 x + 3(y + 1) = 2x + 3y + 3 = s(s(s(2x + 3y))) = s(s(s(f(x; y)))):

Следовательно, функция f(x; y) возникает из примитивно рекурсивных функци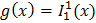й

и 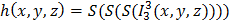операцией примитивной рекурсии и поэтому функция f(x; y) = 2x + 3y является примитивно рекурсивной.