
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поток вектора напряженности электростатического поля. Теорема Гаусса для электростатического поля в вакууме
|
|
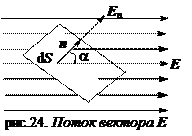 Скалярное произведение векторов E и d S называется потоком вектора напряженности d ФЕ через площадку d S (рис. 1.2.): d ФE = Е∙ d S = Е∙ d S cosa= Еn d S, где a – угол между векторами n и Е; Еn = Е cosa – проекция вектора Е на нормаль n к площадке d S.
Скалярное произведение векторов E и d S называется потоком вектора напряженности d ФЕ через площадку d S (рис. 1.2.): d ФE = Е∙ d S = Е∙ d S cosa= Еn d S, где a – угол между векторами n и Е; Еn = Е cosa – проекция вектора Е на нормаль n к площадке d S.
Если плоская поверхность S перпендикулярна силовым линиям однородного электрического поля, то поток напряженности через нее
ФЕ = Е∙ S.
Для неоднородных полей поток напряженности поля через всю поверхность представится суммой элементарных потоков:
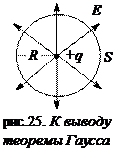
 .
.
Единицей измерения потока вектора напряженности электростатического поля является вольт-метр (В·м). Поток вектора напряженности электростатического поля зарядов q в вакууме (e = 1) через сферическую поверхности радиусом R, охватывающую этот заряд, находящийся в ее центре (рис.25):
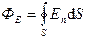 ,
,
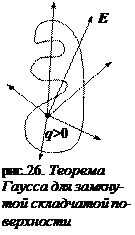 Во всех точках сферы |E| одинакова, и силовые линии перпендикулярны поверхности. Следовательно,
Во всех точках сферы |E| одинакова, и силовые линии перпендикулярны поверхности. Следовательно, 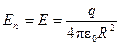 . Площадь поверхности сферы равна 4p R 2. Отсюда
. Площадь поверхности сферы равна 4p R 2. Отсюда
 .
.
На рис. 26 представлена произвольная замкнутая поверхность, охватывающая заряд q > 0. Некоторые линии напряженности то выходят из поверхности, то входят в нее. Нечетное число пересечений сводится к одному: линии, выходящие из поверхности – положительные, а линии, входящие – отрицательные. Если замкнутая поверхность не охватывает заряд, то ФЕ = 0. Если замкнутая поверхность охватывает несколько зарядов, то
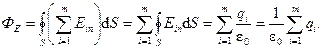
Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на электрическую постоянную e0.
Эта формулировка представляет собой теорему К. Гаусса.
Применяя теорему Гаусса, можно определить напряженности полей, создаваемых заряженными телами различной формы:
1) напряженность поля равномерной бесконечной плоскости 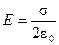 ;
;
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
2) напряженность поля двух бесконечных равномерно заряженных плоскостей 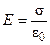 ;
;
3) напряженность поля заряженной сферической поверхности  ,
,
где величина  называется поверхностной плотностью заряда.
называется поверхностной плотностью заряда.
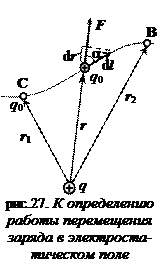 Работа сил электростатического поля при перемещении заряда. Циркуляция вектора напряженности электростатического поля. Потенциальная энергия и потенциал электростатического поля
Работа сил электростатического поля при перемещении заряда. Циркуляция вектора напряженности электростатического поля. Потенциальная энергия и потенциал электростатического поля
При перемещении заряда в электростатическом поле действующие на заряд кулоновские силы совершают работу. Пусть точечный заряд q 0 > 0 перемещается в поле другого точечного заряда q > 0 из точки С в точку В вдоль произвольной траектории (рис.27). При элементарном перемещении заряда на d l эта сила совершает работу d A:
d A = F ·d l = F d l cosa,
где a – угол между векторами F и d l; d l cosa = d r – проекция вектора d l на направление силы F. Таким образом,
d A = F d r,  .
.
Полная работа по перемещению заряда q 0 из точки С в точку В определяется интегралом
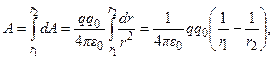
где r 1 и r 2 – расстояния от заряда q до точек С и В. Из полученной формулы следует, что работа, совершаемая при перемещении заряда q 0 в поле заряда q, не зависит от формы траектории движения, а зависит только от начального и конечного положений заряда. Следовательно, электростатическое поле точечного заряда – потенциальное, а действующие в нем силы – консервативные.
Работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е. 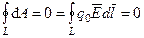 Так как d A = F d l и F = E q 0, то d A = q 0 E d l. Отсюда получаем
Так как d A = F d l и F = E q 0, то d A = q 0 E d l. Отсюда получаем 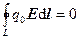 . Если заряд q 0 является единичным положительным точечным, то получим
. Если заряд q 0 является единичным положительным точечным, то получим
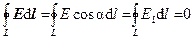 ,
,
где El = E cosa – проекция вектора Е на направление элементарного перемещения d l. Интеграл 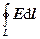 называется циркуляцией вектора напряженности. Таким образом, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Это заключение справедливо для потенциального поля.
называется циркуляцией вектора напряженности. Таким образом, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Это заключение справедливо для потенциального поля.
Работа в таком поле совершается за счет убыли потенциальной энергии:
A = – Δ W п = W п1 – W п2.
Используя формулу работы силы электростатического поля по перемещению заряда, получим
 =
= 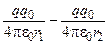 = W п1 – W п2.
= W п1 – W п2.
Анализируя полученное выражение, можно сделать вывод, что потенциальная энергия точечного заряда q 0 в поле заряда q равна
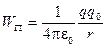 .
.
Если поле создано системой зарядов q 1, q 2,..., qn, то потенциальная энергия заряда q 0:
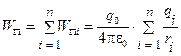 .
.
Потенциальная энергия заряда q 0 зависит от его величины. Однако отношение потенциальной энергии заряда q 0 к его величине является постоянным для данной точки поля и может служить энергетической характеристикой данной точки поля. Отношение 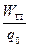 называется потенциалом электростатического поля j:
называется потенциалом электростатического поля j:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
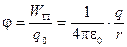 .
.
Потенциал j– скалярная физическая величина, численно равная потенциальной энергии единичного положительного заряда, помещенного в данную точку поля.
Ранее было записано A = W п1 – W п2. Так как W п1 = φ 1 q 0 и
W п2 = φ 2 q 0, то A = q 0(φ 1 – φ 2) и Δ φ = (φ 1 – φ 2) =  .
.
Разность потенциалов Δ φ двух точек поля численно равна работе сил поля по перемещению единичного положительного заряда из точки 1 в точку 2.
Если заряд q 0 перемещать из какой-либо точки поля в бесконечность, то r 2 ® ¥, W п2 = 0 и φ 2 = 0. Тогда работа A ∞ по перемещению заряда q0 в бесконечность:
A ∞ = q 0 φ 1, φ 1 = 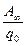 .
.
Потенциал точки поля численно равен работе, совершаемой электрическими силами при перемещении единичного положительного заряда из данной точки поля в бесконечность.
Потенциал точки поля системы зарядов q 1, q 2,..., qn равен алгебраической сумме потенциалов полей всех этих зарядов:
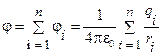 .
.
Единицей потенциала является вольт (В).
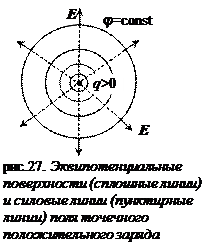 Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями – поверхностями, потенциал всех точек которых одинаков. Если поле создано точечным зарядом, эквипотенциальные поверхности в данном случае – концентрические сферы, а линии напряженности перпендикулярны эквипотенциальным поверхностям (рис.27).
Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями – поверхностями, потенциал всех точек которых одинаков. Если поле создано точечным зарядом, эквипотенциальные поверхности в данном случае – концентрические сферы, а линии напряженности перпендикулярны эквипотенциальным поверхностям (рис.27).
|
|
