Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Давление жидкости на плоскую стенку

Задача определения сил давления жидкости на плоскую стенку заключается в определении равнодействующей P сил давления (рисунок 6) на плоскую стенку, ее направления и точки приложения.

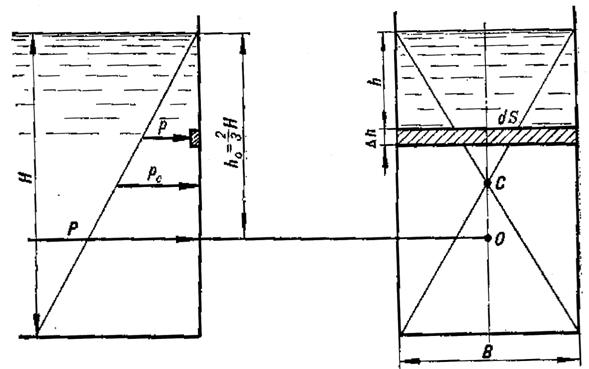
Рисунок 6. Силы, действующие на плоскую стенку

Рассмотрим вертикальную прямоугольную стенку. Пусть ширина стенки равна B, уровень жидкости в сосуде H, а площадь смоченной поверхности рассматриваемой стенки равна S = BH.

Из основного уравнения гидростатики, записанного применительно к избыточному давлению любой точки жидкости,

p_изб = rgh (6)

следует, что эпюра давления p_изб представляет собой прямоугольный треугольник. Причем максимальное избыточное давление на стенку равно давлению на дно сосуда

p_max = rgH (7)

а давление на уровне центра тяжести плоской стенки (точка С) равно

p_c= 0, 5p_max= 0, 5rgH, (7.3)

Учитывая переменный характер давления жидкости по высоте, выделим на текущей глубине h элементарную площадку dS= Bdh и определим элементарную силу давления жидкости на эту площадку

dP= pdS= rghBdh.

Для определения силы давления на всю смоченную поверхность полученное выражение проинтегрируем от 0 до H:

(7.4)

где pc-давление жидкости в центре тяжести (точка С) смоченной поверхности, определяемое по формуле (7.3); S-площадь смоченной поверхности (S=BH).

Формула (7.4) справедлива для плоских стенок любой формы и с любым углом наклона стенки к горизонту.

Очевидно, что направление действия равнодействующей для плоской стенки всегда совпадает с направлением элементарных сил гидростатического давления. Так как эти силы всегда нормальны к плоской стенке, то и равнодействующая сила будет также нормальной.

Точка приложения равнодействующей силы давления p называется центром давления. Центр давления (точка О) в общем случае не совпадает с центром тяжести плоской стенки (точка С) и находится на глубине, соответствующей расположению центра тяжести площади эпюры давлений (см. рис. 7.1). В рассматриваемом случае центр давления находится на глубине

ho= 2/3H.

Если рассматривать дно сосуда, центр тяжести и центр давления совпадают.

Давление жидкости на цилиндрическую стенку

Считается, что в трубопроводе жидкость находится под некоторым давлением p. Допустим, что под действием сил давления труба стремится разорваться по сечениям 1–1 и 2–2 (рис. 7.2).

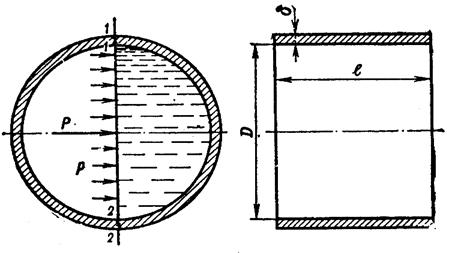
Рисунок 7.2. Силы, действующие на цилиндрическую стенку

Разделим мысленно жидкость в трубопроводе по сечениям 1–1 и 2-2 вертикальной плоскостью, проходящей через предполагаемые сечения разрыва, на две половины и отбросим левую половину.

Для обеспечения равновесия оставшейся части к плоскости раздела необходимо приложить распределенные силы гидростатического давления. Эти силы во всех точках одинаковы (без учета весового давления), нормальны к рассматриваемой плоскости и направлены внутрь рассматриваемого объема. Следовательно, равнодействующая элементарных сил давления равна

P= pDl,

где p – давление в трубопроводе, Па;

Dи l – диаметр и длина трубопровода, м.

При расчете, например, на прочность по разрыву трубопровода следует учитывать общую площадь сечения трубопровода S, по которой происходит разрыв,

S= 2dl.

Таким образом, напряжение растяжения sрв стенках трубы равно

sр= P/S= P/(2dl) = pD/(2dl),

где d– толщина стенки.

Если определяется толщина стенки трубы, то

d= pD/(2 [sр]), (7.5)

где [sр] – допустимое напряжение растяжения.

Силы, действующие на твердое тело, погруженное в жидкость

погруженное в жидкость

На законах статики твердого тела, погруженного в жидкость, базируется теория плавания. Для установления этих законов необходимо определить силы, действующие на твердое тело, погруженное в жидкость.

Рассмотрим некоторый цилиндр С площадью основания S и высотой H, погруженный в жидкость (рис. 5.1).

Определим силы, действующие на основания тела:

на верхнее основание

P1= poS = (po + rgh1)S;

на нижнее основание

P2= p2S = (po + rgh2)S.

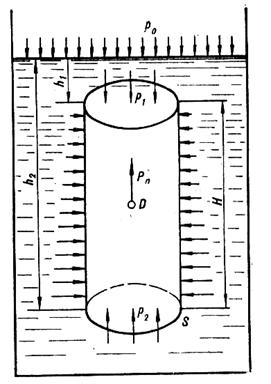
Рисунок 5.1. Силы, действующие на твердое тело, погруженное в жидкость

Так как h2 > h1, то P2 > P1.

Разность сил

Pп= P2- P1=rgS(h2-h1)=rgSH=rgV, (5.1)

где r– плотность жидкости; V = S(h2 - h1) = SH – объем тела, называемыйподъемнойили выталкивающей силой. Эта сила всегда направлена вверх.

Таким образом, подъемная сила, действующая на тело со стороны жидкости, равна силе тяжести жидкости, вытесненной телом. Это – закон Архимеда.

Согласно закону Архимеда из формулы (5.1) следует важный вывод: подъемная сила не зависит от глубины погружения тела в жидкость.

Точка D приложения подъемной силы расположена в центре тяжести вытесненного объема жидкости, называемом центром водоизмещения. Этот центр совпадает с центром тяжести тела (центром массы) только в том случае, когда тело однородно.