Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Следствия закона гидростатического давления

Из закона гидростатического давления вытекают четыре основных следствия, широко используемых в практике.

1. О поверхности равного давления. Плоскость, проведенная в покоящейся жидкости таким образом, что давление во всех ее точках будет одинаковым, называется поверхностью равного давления. Эти поверхности всегда нормальны вектору массовых сил. Поэтому, если необходимо, например, измерить давление в некоторой точке А (рис.4.2), недоступной для установки датчика прибора, то этот датчик может быть установлен в любой другой точке (например, точкеБ), расположенной в плоскости равного давления.

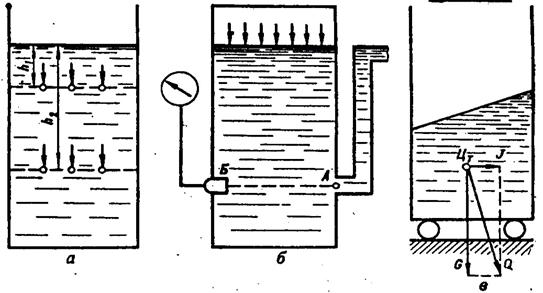
Рисунок 2. Расположение поверхностей равного давления

а– при абсолютном покое; б – установка датчика прибора для измерения давления в точке А; в – при относительном покое

Следствие о поверхностях равного давления позволяет определять положение свободной поверхности жидкости в ее относительном покое. Свободная поверхность жидкости, например, в движущемся прямолинейно сосуде с постоянным ускорением всегда будет расположена нормально к равнодействующей силы тяжести и силы инерции.

2. О передаче поверхностного давления в жидкости. Это следствие называется законом Паскаля и формулируется так: внешнее давление, действующее на свободную поверхность жидкости, передается во все точки жидкости без изменения.

И действительно, в двух произвольно выбранных точках 1 и 2 (рисунок 3) величина давления будет определяться по основному уравнению гидростатики следующими выражениями:

P₁= po + rgh₁;

P₂= po + rgh₂,

Из сравнения этих выражений видно, что поверхностное давление передается в точки 1 и 2 без изменений, а следовательно, оно передается без изменений и во все другие точки жидкости.

Закон Паскаля имеет весьма широкое практическое применение.

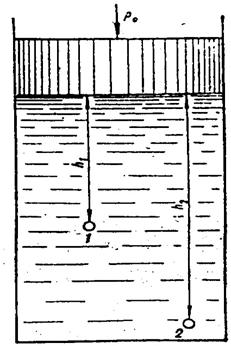
Рисунок 3. Передача поверхностного давления в любую точку жидкости

Он используется при создании различных гидравлических устройств, работающих на принципе передачи давления внутри жидкости. Такими устройствами являются гидрообъемные передачи: гидравлические домкраты, гидравлические приводы управления и собственно гидрообъемные передачи, работающие в трансмиссиях многих машин.

3. О сообщающихся сосудах. Уровни несмешивающихся жидкостей в сообщающихся сосудах зависят от поверхностных давлений и плотностей жидкостей.

Пусть два сообщающихся сосуда заполнены несмешивающимися жидкостями с плотностями r1и r2, причем линия их радела О – О находится в левом сосуде (рисунок 4).

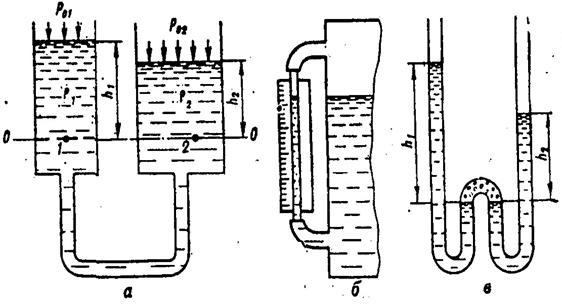
Рисунок 4. Сообщающиеся сосуды и их использование

а– принципиальная схема; б – мерная стеклянная трубка; в – прибор для определения плотности жидкости

Очевидно, что в точках 1 и 2 гидростатические давления будут равны, т.е. p1 = p2 или

po1+r1gh1= po2+ r2gh2 (5)

Это равенство является математическим выражением равновесия жидкостей в сообщающихся сосудах в общем случае. В частном случае при равенстве плотностей r1и r2и поверхностных давлений po1 и po2 следует, что h1 = h2, т.е. уровни одной и той же жидкости в сообщающихся сосудах одинаковы и не зависят от формы сосудов.

По принципу сообщающихся сосудов устроены мерные стеклянные трубки, простейшие приборы для определения плотности жидкости и др.

4. О гидростатическом парадоксе. Явление гидростатического парадокса заключается в том, что давление на дно сосуда не зависит от формы сосуда. Возьмем, например, несколько сосудов различной формы (рисунок 5) с одной и той же жидкостью и определим давление на дно сосудов:

для цилиндрического сосуда и сосуда с вертикальной трубой имеем

p1= p2= po+ rgH;

для сосуда с наклонной трубой имеем

p3= po + r1gh1+ r2gh2=po + rgH

Так как дно сосуда является поверхностью равного давления, то во всех его точках давление будет одно и то же

p1= p2 = p3 =po + rgH.

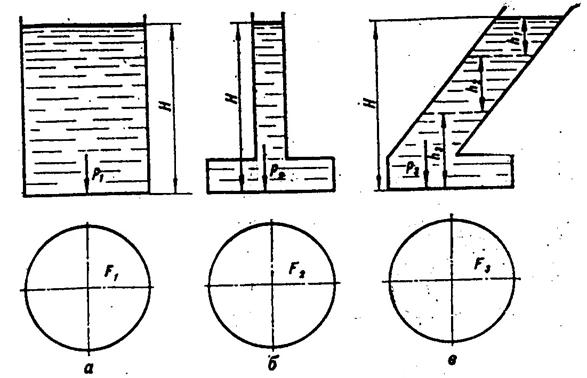
Рис.4.5. К вопросу о гидравлическом парадоксе

а– цилиндрический сосуд; б – сосуд с вертикальной трубой;

в– сосуд с наклонной трубой