Сравнение рекурсии и итерации

Рекурсия:

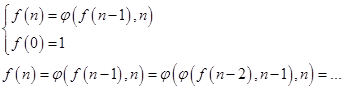
При прямом ходе вычисление значения функции откладывалось, при этом значение функции для одного аргумента заменялось на значение выражения, в котором нужно было вычислить значение той же функции, но для другого аргумента. Вычисляемая функция откладывалась до тех пор, пока в выражении не появится значение функции, которое было определено. После подстановки известного значения, происходил возврат к отложенным вычислениям.

Итерация:

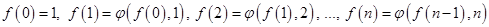
После определения начального значения 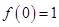, повторяются одни и те же действия, при которых, значения, полученные на предыдущем шаге, используются для вычисления очередного значения функции.

При выполнении сравнения можно учитывать разные критерии.

1. Самый распространенный – это эффективность алгоритма. В данном случае под эффективность понимаются время процессора и объем занятой программой (и данными) памяти. В данном случае не трудно заметить явное преимущество итеративного метода по сравнению с рекурсивным.

2. Сложность написания и отладки программы. По существу это вопрос о затратах труда программиста. Сравнение двух текстов показывает, что рекурсивная программа пишется автоматически на основе поставленной задачи, в то время как итеративная требует преобразования задачи и " изобретения" алгоритма, введение дополнительных переменных, отсутствовавших в постановке задачи, и неочевидных операций. Поэтому, с этой точки зрения, рекурсивный алгоритм предпочтительнее итеративного.

Вывод: В тех случаях, когда не требуется получать очень быстрый отклик программы, рекурсия помогает сэкономить на разработке программы.

на примере чисел Фибоначчи:

рекурсия:

function Fr(n: integer): integer;

begin if n=1 or n=2 then Fr: =1

else Fr: =Fr(n-1)+Fr(n-2);

end;

итерация:

function Fi(n: integer): integer;

var i, n1, n2, result: integer;

begin n1: =1, n2: =1; {установка начальных значений}

result: =1; {на тот случай, если n=1 или 2}

for i: =3 to n do {не выполняется если n< 3}

begin result: =n1+n2; {соот-ет осн формуле чисел Фиб}

n2: =n1; {сдвиг значений на один индекс}

n1: =result; {----||----}

end;

Fi: =result; {установление значения функции}

end;