Procedure процедура_1

….

if … then процедура_1

….

End;

Косвенная рекурсия образуется цепочкой процедур, и эта цепочка замыкает себя в рекурсивное кольцо, например:

Procedure процедура_1

….

… процедура_2

….

End;

Procedure процедура_2

….

… процедура_3

….

End;

Procedure процедура_3

….

… процедура_1

End;

· Для вычисления сложности рекурсивных алгоритмов используется рекуррентное уравнение:

T_a(X)=T_a(f(X))+ T_f(X)+ T_h(X)+ T_с(X, S)

T_a(S)=T_c(S, S)+ T_s(S)

Здесь

T_a(X) – общая сложность рекурсивного алгоритма

T_a(f(X)) – сложность предыдущего уровня рекурсии

T_f(X) – сложность вычисления аргументов при рекурсивном вызове процедуры

T_h(X) – сложность нерекурсивных вычислений

T_с(X, S) – сложность операции сравнения

T_s(S) – сложность вычисления нерекурсивного начального значения

T_c(S, S) – сложность операции сравнения для нерекурсивного начального значения

Пример:

Function F(n);

begin

If (n=0) or (n=1) {проверка возможности прямого вычисления}

Then

F: = 1

Else

F: =n*F(n-1); {рекурсивный вызов функции}

End;

X = x,

S = 1, x = 1

f(X)=X-1, FACTORIAL (x-1)

Tf(X)=1, FACTORIAL (x-1)

Th(X) = 2, FACTORIAL: = x * FACTORIAL (x-1)

Tc(X, S)=l, x = 1

Ts(S) = 1. FACTORIAL: = 1

Таким образом, система уравнений превращается в

Тa(x) = Тa(х-1)+4, Тa(1) = 2.

Ее решение – Тa(x) = 4х-2.

В случае косвенной рекурсии рекуррентное уравнение имеет вид:

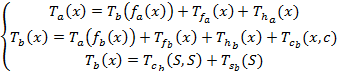
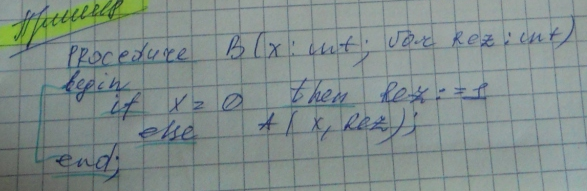
12) 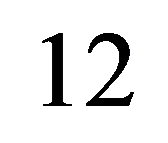Оптимизация алгоритмов. Примеры.

Поиск алгоритма min сложности – оптимизация алгоритма.

Одна из задач, которая обычно ставится при разработке алгоритмов и программ - минимизация требуемых программой ресурсов. Особенно это касается системного программного обеспечения: программ операционной системы, трансляторов, систем управления базами данных и знаний и т. д., т.е. программ, имеющих большое количество пользователей и испытывающих как товар, большую конкуренцию на рынке программных средств.

Существует несколько самостоятельных аспектов оптимизации программ, из которых выделим два:

· оптимизация, связанная с выбором метода построения алгоритма;

· оптимизация, связанная с выбором методов представления данных в программе.

Первый вид оптимизации имеет глобальный характер и (при удачной оптимизации) ведет к уменьшению порядка функции сложности - например, замена алгоритма с Тa(V) = O(F^S) на алгоритм с Ta(V) = O(V⁴). Он зависит от того, как задача разбивается на подзадачи, насколько это разбиение свойственно самой задаче или является только искусственным приемом.

Второй вид оптимизации, не меняя структуры программы в целом, ведет к экономии памяти и/или упрощению работы со структурами данных, повышению эффективности вспомогательных процедур, обеспечивающих " интерфейс" между прикладным уровнем (на котором мыслим в терминах высокоуровневых объектов - графов, матриц, текстов и т. д.) и машинным уровнем, поддерживающим простейшие типы данных (числа, символы, указатели). Результатом этого обычно является уменьшение коэффициентов при некоторых слагаемых в функции сложности (при удачной оптимизации - при наиболее значимом слагаемом), но порядок функции сложности остается тем же.

Пример: вычисления числа Фибоначчи через формулу:

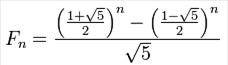
13) Понятие сложности задачи и классы сложности задач. Понятия сводимости, полиномиальная сводимость.

Задачи:

1. массовые (список параметров и формулировка условий)
2. частные (формальные параметры заменяются фактическими)

сложность задачи – сложность самого простого алгоритма. Поиск алгоритма min сложности – оптимизация алгоритма.

Детерминированные вычисления – обычный, классический способ.

Недетерминированные вычисления – существует в нескольких параллельно работающих экземплярах. Недетерминированный вычислитель исполняет недетерминированные алгоритмы. Разрешаем шаги с неоднозначным результатом – шаги, вырабатывающие сразу несколько значений для одной переменной. Эти значения могут использоваться:

1. параллельно выполняющиеся процессы.
2. угадать, какое из значений, полученных на данном шаге, является правильным и использовать только его.

Классы сложности задач:

1. полиномиальные-их временная сложность ограничивается сверху некоторым полиномом.
2. экспоненциальные – в общем случае требуется кол-во операций, увеличивающееся с ростом n по крайней мере експоненциально.
3. NP – задачи, которые можно решить за полиномиальное время на недетерминированном вычислителе

Задача Q сводится к задаче Р за полином.время, если сущ-ет детерминированный полиномиальный алгоритм, преобразовывающий произвольный частный случай задачи Р так, что ответом для данного случая задачи Q является «да» тогда и только тогда, када ответом на соответсвующий случай задачи Р также является «да».

вход для Q Вход для Р ответ Р Ответ Q

Полиномиальная сводимость – детерминированный полиномиальный алгоритм сводит одну задачу к другой

NPC – подкласс NP, любая задача NP сводится к ним

14) Методы сортировок: сортировка массивов простыми включениями, сортировка массивов простым выбором, сортировка обменами. Анализ сложности алгоритмов сортировки.

Сортировка – процесс перегруппировки заданного множества объектов в некотором определенном порядке. Цель сортировки – облегчить последующий поиск элементов в таком упорядоченном (отсортированном) множестве. Сортировку массивов называют внутренней сортировкой, т.к. поскольку массивы хранятся в быстрой, оперативной, внутренней памяти ЭВМ, допускающей случайный (прямой) доступ к элементам.

При анализе сложности алгоритмов сортировки будем учитывать только операции сравнения и пересылки записей.

Сортировка обменами:

Производится последовательное упорядочение смежных пар элементов массива: x [1] и x [2], x [2] и x [3], … x [ N -1] и x [ N ]. Если первый элемент больше второго, то элементы переставляются. В итоге, после N –1 сравнения максимальное значение переместится на место элемента X [ N ], т.е. " вверху" оказывается самый " легкий" элемент – отсюда аналогия с пузырьком. Следующий проход делается до второго сверху элемента (X [ N –1]), таким образом второй по величине элемент поднимается на правильную позицию и т.д. Таким образом, нужно выполнить данную процедуру N –1 раз.

При первом прохождении нужно сравнить N –1 пар элементов, при втором – N –2 пары, при k -м прохождении – N ‑ k пар.