
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Числовые характеристики дискретной случайной величины
|
|
Полную характеристику случайной величины X можно дать с помощью закона распределения и числовых характеристик, к которым относятся математическое ожидание, дисперсия и среднее квадратическое отклонение.
Математическим ожиданием случайной величины X называется ее среднее значение.
Математическое ожидание определяет положение центра распределения и для дискретной случайной величины вычисляется по формуле:
 (1)
(1)
Математическое ожидание обозначается буквой “ a ” и имеет размерность рассматриваемой случайной величины.
Математическое ожидание в некоторых случаях не может в достаточной степени охарактеризовать случайную величину, поскольку разброс ее значений относительно центра распределения бывает достаточно велик.
Для оценки рассеивания значений случайной величины от среднего значения 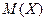 используют дисперсию.
используют дисперсию.
Дисперсией случайной величины X называется математическое ожидание квадрата разности между случайной величиной X и ее математическим ожиданием 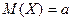 .
.
Дисперсия для дискретной случайной величины вычисляется по формуле:
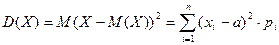 . (2)
. (2)
Из свойств дисперсии, приведенных ниже, может быть получена другая формула для вычисления  :
:
 , где
, где  . (3)
. (3)
Дисперсия случайной величины имеет размерность квадрата этой случайной величины.
Средним квадратическим отклонением (или разбросом, или стандартным отклонением) называется величина, вычисляемая как корень квадратный из дисперсии:
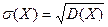 . (4)
. (4)
Среднее квадратическое отклонение имеет размерность самой случайной величины.
Замечание 1. Если случайная величина X распределена по биномиальному закону с параметрами n и p, то для расчета математического ожидания и дисперсии можно применять следующие формулы:
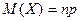 ,
, 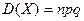 . (5)
. (5)
Замечание 2. Если случайная величина X распределена по закону Пуассона, то:
 . (6)
. (6)
Пример 5. У дежурного гостиницы в кармане 5 разных ключей от разных комнат. Вынув наугад ключ, он пробует открыть дверь ближайшей комнаты. Сколько раз в среднем ему придется пробовать открывать эту комнату, если проверенный ключ не кладется обратно в карман?
Решение. Рассмотрим случайную величину X – число попыток открыть дверь ближайшей комнаты, которая может принимать значения 1, 2, 3, 4, 5. Требуется найти 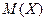 . Составим сначала закон распределения случайной величины X. Введем события:
. Составим сначала закон распределения случайной величины X. Введем события:
 - “дверь открыта с i – ой попытки”,
- “дверь открыта с i – ой попытки”, 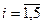 ;
;
 - “дверь не открыта с i – ой попытки”,
- “дверь не открыта с i – ой попытки”, 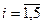 .
.
 и
и  - зависимые события, т.к. проверенный ключ не кладется обратно в карман.
- зависимые события, т.к. проверенный ключ не кладется обратно в карман.
По теореме умножения для зависимых событий, находим:



Проверка:  - верно.
- верно.
Закон распределения случайной величины X имеет вид:
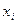
| |||||

| 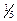
| 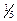
| 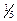
| 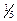
| 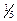
|
Находим математическое ожидание:
 - столько раз в среднем дежурному придется открывать эту комнату.
- столько раз в среднем дежурному придется открывать эту комнату.
Ответ: 3 раза.
Приведем свойства математического ожидания:
1. Математическое ожидание постоянной величины равно этой величине:
 , где
, где  .
.
2. Постоянный множитель можно выносить за знак математического ожидания:
 .
.
3. Математическое ожидание суммы случайных величин равно сумме математических ожиданий этих величин:

4. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих величин:
 .
.
5.  , где
, где  .
.
Приведем свойства дисперсии:
1. Дисперсия постоянной величины равна нулю:
 , где
, где  .
.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
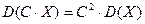 .
.
3. Дисперсия суммы (разности) независимых случайных величин равна сумме их дисперсий:
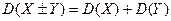 .
.
Пример 6. Дискретная случайная величина задана законом распределения:
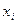
| -1 | |||

| 0, 2 | 0, 3 | 0, 1 | 0, 4 |
Найти  ,
, 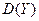 ,
,  , где
, где 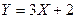 .
.
Решение. Вычисляем сначала числовые характеристики случайной величины X:

Пользуясь свойствами математического ожидания и дисперсии, находим числовые характеристики случайной величины Y:

Ответ: 
Пример 7. Найти значения случайной величины 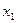 и
и 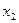 (
(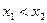 ), заданной законом распределения, если
), заданной законом распределения, если  ,
, 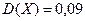 .
.
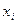
| 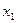
| 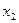
|

| 0, 1 | 0, 9 |
Решение. По формуле (1) математическое ожидание  , а по условию задачи
, а по условию задачи  , следовательно, получаем равенство
, следовательно, получаем равенство  или
или 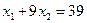 .
.
По формуле (3) дисперсия равна  , а по условию задачи
, а по условию задачи 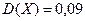 , тогда получаем, что
, тогда получаем, что  ,
, 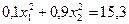 ,
, 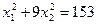 .
.
Таким образом, получаем систему двух уравнений с двумя неизвестными:

Из первого уравнения системы выражаем переменную  и подставляем ее во второе уравнение:
и подставляем ее во второе уравнение:
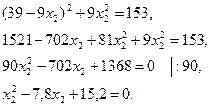
Решая квадратное уравнение, получаем, что 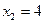 и
и  .
.
При 
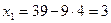 ; при
; при 
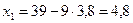 . Итак, система имеет два решения (3; 4) и (4, 8; 3, 8), но, так как,
. Итак, система имеет два решения (3; 4) и (4, 8; 3, 8), но, так как, 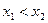 , то искомые значения случайной величины
, то искомые значения случайной величины  ,
,  .
.
Ответ:  ,
,  .
.
|
|