Цветовой график МКО

С целью устранения этих недостатков на VIII сессии Международной комиссии по освещению (МКО) в 1931 году была принята международная система классификации цветов.

Были введены три нереальных (их невозможно увидеть) основных цвета XYZ.

В основу построения системы положены следующие условия:

1. Кривые смешения не должны иметь отрицательных координат, т.е. все реальные цвета должны иметь положительные коэффициенты в уравнении смешения цветов.

.

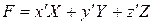2. Количественная характеристика цвета должна полностью определяться его координатой (Y).

3. Координаты белого цвета равного энергетического излучения должны быть равны.

Цвет F в системе МКО изображается точкой с координатами x´ y´ z´ (см. рис) или вектором, проведенным в эту точку из начала координат.

Начало всех векторов лежит в точке черного цвета 0. Основной цвет Y задается таким образом, чтобы его распределение энергии совпадало в точности с кривой чувствительности глаза.

Плоскости Y= const являются плоскостями постоянной яркости (интенсивности) – на них заканчиваются векторы всех цветов, имеющих равную яркость.

Угловое положение вектора определяет качественную характеристику цвета, т.е. его цветность. Чтобы от цвета перейти к цветности, надо исключить количественную характеристику.

Для этого введем относительные координаты.

; ; .

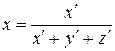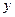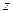, , - называют координатами цветности или трехцветными коэффициентами.

Отметим, что , по этому цветность (качество цвета) однозначно определяется двумя из них (x и z). Она может быть изображена точкой на плоскости, в частности на равно яркой плоскости.

Однако удобно пользоваться плоскостью единичных цветов проведенной через концы ортов, т.е. точки с координатами

x=0, y=0, z=1;

x=0, y=1, z=0;

x=1, y=0, z=0.

Эта плоскость определяется уравнением

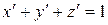
Следы пересечения единичной плоскости с координатными плоскостями образует цветовой треугольник.

Каждая точка в нем представляет определенную цветность. На рисунке в частности можно показать линию, на которой располагаются цветности монохроматических (спектральных) цветов. Рассматриваемый треугольник равносторонний, удобнее же пользоваться прямоугольным, поэтому его проектируют на плоскость ХОY так, чтобы точка (z=1, x=0, y=0,) совпала с 0.

В результате получается широко известный цветовой график МКО, который обладает следующими особенностями.

1. Координаты цветности (трехцветные коэффициенты) x и y образуют прямоугольную систему координат.

2. На линии 0 x расположены цвета с нулевой яркостью (y=0 т.е. Y =0). Однако это не значит, что координата 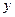пропорциональна яркости.

3. Абсолютно чистые цвета спектра лежат на криволинейной границе, где указываются их длины волн.

Внутри и на границе подковообразной области содержатся все видимые цвета, при этом, все воспринимаемые цвета, имеющие одинаковую цветность, но различные яркости, отображаются в одну точку внутри области.

4. Опорный белый цвет, являющийся аппроксимацией солнечного цвета располагается вблизи точки с координатами

x _c = y _c = z _c = 1/3.

Цветовой график МКО оказывается полезным во многих случаях.

Он позволяет измерить доминирующую длину волны и чистоту любого цвета, уравнивая цвет при помощи смеси трех основных цветов МКО.

Например, цвет N может быть получен в результате смешения белого цвета (источник цвета С) и чистого спектрального цвета, расположенного в точке _.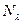

Таким образом, 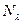определяет доминирующую длину волны. Отношение отрезков

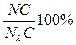- задает чистоту цвета N.

Чем ближе N к С, тем больше белого входит в состав N и тем самым менее чистым является этот цвет.

Некоторые цвета, такие как К нельзя определить с помощью длины волны. Такие цвета называют не спектральными. В этих случаях говорят, что доминирующая длина волны является дополнительной к длине волны точки D.

Дополнительными цветами называются цвета, смесь которых порождает белый. В нашем случае около 565нм. Чистоту цвета К можно определить через отношение длин отрезков

.

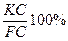С помощью дополнительной к доминирующей длины волны выражаются пурпурные и пурпурно-красные цвета, которые расположены в нижней части графика МКО.

Другим применением цветового графика МКО является задание цветовых диапазонов или цветовых охватов.

Смешиванием двух цветов, например B и G, можно, путем подбора их относительных яркостей, получить любой цвет, лежащий на прямой, которая соединяет два смешиваемых цвета.

Добавление к различным смесям цветов B и G третий цвет R можно получить путем подбора относительных яркостей, охват всех цветов, расположенных в треугольнике RGB.

Достаточно взглянуть на форму цветового графика и станет ясно, почему аддитивной смесью спектральных видимых цветов красного, зеленого и синего нельзя уравнять все цвета: ни один из треугольников, вершины которого находятся внутри видимой области, не будет полностью покрывать всю видимую область. Чистые зеленые и голубые цвета оказываются вне площади такого треугольника и не могут быть воспроизведены. Однако, такие чистые цвета в природе встречаются крайне редко.

Таким образом, цветное изображение на цветном телевизионном дисплее может быть получено при помощи аддитивного смешения трех цветных свечений люминофоров в одной трехцветной ЭЛТ. Для оценки используется цветовой график МКО.