Однокристальные сцинтилляционные гамма-спектрометры

Коллимированный пучок γ -квантов направляется на кристалл сцинтилляционного счетчика, импульсы которого после усили­теля попадают на амплитудный многоканальный анализатор. Типичные распределения амплитуд импульсов, полученные с кристаллом Nal(Tl) диаметром и высотой 40 мм, показаны на рис. 10.2.

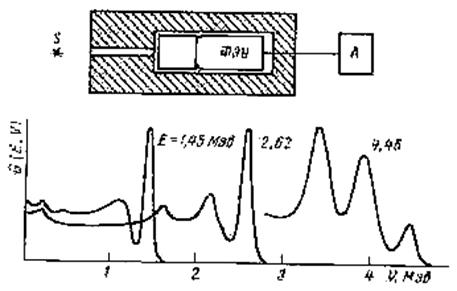
Рис. 10.2. Блок-схема однокристального сцинтилляционного спектрометра и его функция отклика для γ -квантов

В амплитудных распределениях виден четко выраженный максимум – пик полного поглощения, обусловленный фотоэлектри­ческим поглощением γ -квантов и их многократным комптоновским взаимодействием в кристалле с последующим поглощением. Между непрерывным распределением, обусловленным комптоновским рассеянием, и пиком полного поглощения имеется провал, связанный с тем, что при однократном рассеянии γ -квант не может передать всю свою энергию электрону. Расстояние между пиком полного поглощения и границей комптоновского распределения составляет Е _γ /(1+ 2 Е _γ / m ₀ c ²) (т.е. около 250 кэв).Чем выше энергия γ -квантов, тем больше абсолютный разброс по амплитудам импульсов. Поэтому с ростом энергии γ -квантов пик полного поглощения все хуже и хуже отделяется от непрерывного комптоновского распределения и все большее значение приобретает эффект образования пар, который приводит к появлению еще двух пиков в амплитудном распределении импульсов. Эти пики отстоят от пика полного поглощения в шкале энергий на 0, 51 и 1, 02 Мэв. С дальнейшим ростом энергии γ -квантов эти пики все хуже разделяются и при энергиях, выше 5…7 Мэвпрактически сливаются в один широкий максимум.

В приведенных амплитудных распределениях видны пики при энергиях около 250 кэв. Их появление связано с обратным рассеянием γ -квантов на упаковке кристалла и колбе фотоумножителя. Чтобы γ -квант создал амплитуду в этой области энергии, он должен или рассеяться в кристалле на малый угол, или пройти через кристалл без взаимодействия, рассеяться на упаковке кристалла или колбе фотоумножителя на угол, больший 90°, и погло­титься в кристалле. Последний процесс приводит к образованию максимума в амплитудном распределении, поскольку энергия обратно рассеянных квантов слабо зависит от угла рассеяния. Приведенные на рис. 10.2 функции отклика G (Е, V)оказываются довольно сложными, и это затрудняет получение спектров γ -квантов по измеренным амплитудным распределениям импульсов. Как уже отмечалось ранее, функции отклика будут иметь более близкий к распределению Гаусса вид, если увеличи­вать размеры кристаллов. Этому же способствует применение коллиматоров, которые позволяют выделить узкий пучок γ -квантов и направить его в центр кристалла.

При измерениях спектров γ -квантов с помощью однокристальных сцинтилляционных спектрометров основная проблема заключается в преобразовании амплитудного распределения импульсов в энергетические спектры, т.е. в решении интегрального уравнения. Для этого, во-первых, с особой тщательностью следует определить функции отклика G (E, V)и, во-вторых, найти подходящий метод решения интегрального уравнения.

Функцию отклика G (E, V)можно определить расчетно и экспе­риментально. Экспериментальное определение G (E, V)имеет в сравнении с расчетным преимущества: в расчетах не удается учесть многие эффекты, такие, как уход электронов из кристалла, рассеяние у-квантов на предметах, окружающих кристалл, и т.д. В области энергий γ -квантов ниже 3 Мэв имеется достаточное число радиоактивных источников γ -квантов, испускающих одну или две группы моноэнергетических γ -квантов. В области более высоких энергий экспериментальное определение G (E, V) затруднено, поскольку нет удобных источников моноэнергетического излучения. Здесь часто G (E, V) определяют расчетным путем. Экспериментальное определение G (E, V) сводится к измерению амплитудных распределений импульсов спектрометра с различными источниками γ -квантов, внесению поправок в измеренные распределения на рассеяние γ -квантов в источнике и окружающих его предметах, на тормозное излучение, образующееся в источнике, и т.д. Полученные амплитудные распределения нормируют с учетом эффективности спектрометра, т.е. требуют, чтобы

∫ G (E, V) dV = ε (E),

где ε (Е) – эффективность сцинтилляционного счетчика, определение которой дано выше.

Поскольку эффективность и ряд поправок можно рассчитать с достаточной точностью, то для определения функций отклика не требуются источники с известной активностью, т.е. можно проводить относительные измерения.

Энергетическое разрешение однокристальных сцинтилляционных спектрометров зависит от качества кристаллов и фотоумножителей и в первом приближении обратно пропорционально (более подробно этот вопрос уже обсуждался выше).

Использование неорганических кристаллов, таких, как Nal(Tl) и CsI(Tl), не всегда возможно, если исследуемое γ -излучение сопровождается нейтронами. Нейтроны, поглощаясь в иоде (сечение радиационного захвата нейтронов с энергией около 100 кэвравно 0, 1 барн), создают γ -кванты, энергии которых лежат в области до 6 Мэв.Кроме того, нейтроны с энергиями выше 0, 5 Мэвпри неупругом рассеянии также образуют γ -кванты,, а сечение неупругого рассеяния достигает примерно 1 барн, т.е. сравнимо с сечением взаимодействия γ -квантов с атомами. Поэтому неорганические кристаллы практически нельзя использовать для спектрометрии γ -квантов, если последние сопровождаются нейтронами, потоки которых сравнимы с потоками γ -квантов.

Исследование спектров γ -квантов при большом нейтронном фоне можно проводить с помощью сцинтилляционных спектрометров с органическими кристаллами стильбена. В составе кристалла водород и углерод. Они имеют малые сечения радиационного захвата, а неупругое рассеяние нейтронов возможно лишь на углероде при энергии нейтронов выше 4, 4 Мэв (энергия первого возбужденного состояния ядра ¹²С). Но нейтроны с большой вероятностью регистрируются в органических кристаллах в результате упругого рассеяния на ядрах водорода. Сечение взаимодействия γ -квантов с атомами и сечение упругого рассеяния нейтронов близки по порядку величин, и поэтому сцинтилляционный счетчик с органическим кристаллом регистрирует нейтроны и γ -кванты примерно с одинаковой эффективностью. Последнее обстоятельство затрудняло использование спектрометров с органическими кристаллами для нейтронной и гамма-спектрометрии.

Брукс и Оуэн предложили способы разделения импульсов от электронов и протонов в органических кристаллах по форме сигналов. Во многих органических сцинтилляторах (в том числе и в стильбене) временное распределение фотонов люминесценции можно представить в виде суммы двух экспонент со значительно отличающимися постоянными τ. Отношения интенсивностей медленной и быстрой компонент отличаются при возбуждении кристалла электронами и протонами. Это позволяет разделять импульсы, созданные протонами и электронами. В настоящее время имеется большое количество схем разделений. Идею разделения поясним на схеме Брукса.

На рис. 10.3 показана блок-схема разделения «протонных» и «электронных» импульсов.

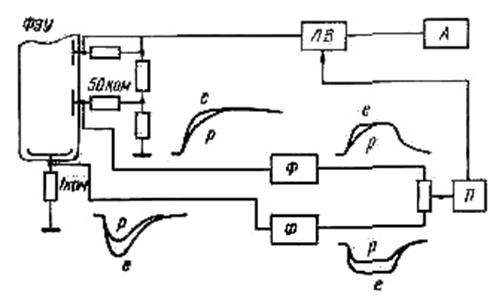
Рис. 10.3. Схема разделения импульсов, созданных электронами и протонами: ЛВ – линейные ворота; А – анализатор; D –дискриминатор; ФЭУ– фотоумножитель; Ф– формирователь

С анода фотоумножителя снимается импульс напряжения с сопротивления порядка 1 к ом, а с динода – с сопротивления порядка 50 к ом. Если в кристалле будут созданы равные по интенсивности световые вспышки электроном и протоном, то формы импульсов на диноде будут несколько отличаться по переднему фронту (у электронного импульса фронт будет несколько меньше, поскольку отношение быстрой компоненты к медленной у него больше, чем при возбуждении кристалла протонами), а амплитуды импульсов будут одинаковы. На аноде электронный импульс будет иметь большую величину, чем протонный, так как малая величина RC в анодной цепи приводит к тому, что максимальное значение амплитуды импульса оказывается пропорциональным интенсивности быстрой компоненты. С динода и анода импульсы поступают на формирователи, после которых они имеют одинаковые длительности, а электронные импульсы с анода и динода – кроме того, и одинаковые амплитуды. Оба сформированных таким образом импульса складываются, и их сумма оказывается в случае регистрации протонов значительно больше, чем при регистрации электронов. Суммарный импульс попадает на дискриминатор. Наличие импульса на выходе дискриминатора означает, что произошла регистрация нейтрона (протон отдачи), а его отсутствие (в идеальном случае) – регистрация γ -кванта (электрон). В спектрометрах импульс на анализатор снимают с какого-либо (например, предпоследнего) динода и направляют на анализатор через так называемые линейные ворота, которые могут пропускать импульс на анализ или при наличии импульса с дискриминатора (совпадения во времени), или при его отсутствии (антисовпадения). Такие схемы разделения позволяют уверенно регистрировать только γ -кванты с энергиями выше 100…300 кэвпри потоках нейтронов, превышающих потоки γ -квантов даже в 100…1000 раз. Возможна и регистрация только нейтронов с энергиями выше 300…500 кэвпри потоках γ ‑ квантов, превышающих потоки нейтронов в сотни и более раз. Спектрометры с кристаллом стильбена и схемой разделения в последнее время стали использоваться для исследования спектров γ -квантов, дискретных и особенно непрерывных. Функция отклика в таких спектрометрах представляет собой непрерывное распределение с достаточно резкой границей и обусловлено в основном однократным комптоновским рассеянием γ -квантов в кристалле. Изучение спектров γ -квантов с помощью спектрометров с органическими кристаллами также требует обязательного преобразования измеренного амплитудного распределения в энергетические спектры.

Многокристальные сцинтилляционные гамма-спектрометры

Многокристальные сцинтилляционные гамма-спектрометры используют в основном потому, что в них удается получить функцию отклика, по своей форме близкой к распределению Гаусса. Правда, эффективность многокристальных спектрометров оказывается много меньше, чем эффективность однокристальных. Однако успех многих исследований определяется не столько эффективностью спектрометра, сколько качеством функции отклика.

Комптоновские сцинтилляционные гамма-спектрометры. Блок-схема сцинтилляционного комптоновского спектрометра показана на рис. 10.4.

Рис. 10.4. Блок-схема комптоновского спектрометра: (а) – комптоновский спектрометр; (б) – спектрометр со сложением импульсов; (в) – функция отклика комптоновского спектрометра (пунктир) и спектрометра со сложением импульсов (сплошная линия) (в). СС – схема совпадений; Σ –схема сложения амплитуд импульсов; ЛВ – линейные ворота; А – анализатор.

Коллимированный пучок γ -квантов направляется на кристалл (его называют центральным), в котором может происходить комптоновское рассеяние γ -квантов. Импульсы с центрального сцинтилляционного счетчика поступают на анализатор амплитуд импульсов только в том случае, если рассеянный в центральном кристалле γ -квант регистрируется во втором (боковом) кристалле. Такой отбор событий осуществляется с помощью схемы совпадений и линейных ворот, которые пропускают импульс на анализатор, если схема совпадения вырабатывает импульс. Таким образом, на анализ попадают импульсы, образующиеся при рассеянии γ -квантов в центральном кристалле под определенным углом. Амплитуда выбранных таким способом импульсов пропорциональна энергии электронов отдачи:

.

Схема расположения кристаллов и их размеры определяют основные параметры спектрометра – эффективность и энергетическое разрешение. Эффективность спектрометра пропорциональна вероятности рассеяния 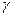-кванта в центральном кристалле в направлении бокового кристалла. Эта вероятность

,

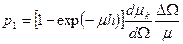где 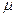и 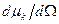– полный линейный коэффициент ослабления 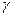-квантов в кристалле и дифференциальное сечение комптоновского рассеяния; 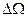– величина телесного угла, определяемого размерами кристаллов и расстоянием между ними. Для того чтобы произошел акт совпадения, рассеянный 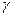-квант должен пройти центральный кристалл без взаимодействия (эта вероятность равна р ₂ = ехр(– 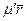), где 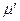– линейный коэффициент ослабления рассеянных 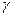-квантов в кристалле; – их средний путь в центральном кристалле) и зарегистрироваться в боковом (эта вероятность равна p ₃ = [1 – ехр(– 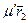)], где r₂ – средний путь 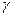-кванта в боковом кристалле). Таким образом,

.

Записанное выражение для эффективности комптоновского спектрометра не совсем точно, поскольку вероятности р₂ и р₃ записаны со средними значениями путей рассеянных фотонов в боковом и центральном кристаллах, что справедливо при небольших размерах кристаллов и малых телесных углах .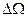

Эффективность спектрометра существенным образом зависит от произведения 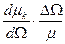, которое весьма чувствительно к форме кристалла. Центральный кристалл выгодно выбирать с малым радиусом и большой высотой, а боковой кристалл – в виде кольца. Чем ближе расположены кристаллы (т.е. чем больше 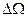) и чем меньше величина угла 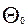, тем больше эффективность, поскольку dμ _k /dΩ имеет наибольшие значения при малых значениях 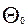. Однако величины 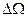и 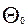существенно влияют и на энергетическое разрешение.

Энергетическое разрешение комптоновского спектрометра зависит не только от свойств центрального сцинтилляционного счетчика, но и от величины углов 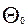и 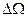. Действительно, чем меньше выбран угол 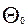, тем меньшую энергию будут иметь электроны в центральном кристалле при рассеянии 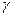-квантов в направлении бокового и тем хуже будет энергетическое разрешение. Рост телесного угла 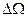увеличивает интервал углов вблизи 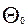, под которыми рассеянные фотоны могут попадать в боковой кристалл, и, следовательно, также ухудшает энергетическое разрешение. Таким образом, увеличение эффективности спектрометра может ухудшать энергетическое разрешение.

Чтобы найти оптимальное соотношение между эффективностью спектрометра и его энергетическим разрешением, сначала определим оптимальное значение угла 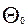. Следовало бы выбрать такое значение угла 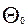, при котором dΘ /dE было бы максимальным. Для этого найдем максимум производной в функции угла 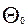. Оказывается, что при заданных значениях Е функция dS/dE_e имеет два максимума пр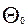и = 0 и 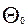=180°. При 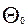= 0 энергия электронов отдачи мала и энергетическое разрешение будет плохим. Поэтому наилучшие характеристики спектрометра будут при выборе углов 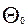, близких к 180°, что позволит при заданном энергетическом разрешении иметь максимальный телесный угол .

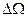Величину телесного угла 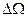имеет смысл выбирать такой, чтобы неопределенность в направлении рассеянного γ -кванта 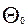± 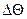не влияла на величину АЕ_е/Е_е, определяемую свойствами сцинтилляционного счетчика.

Если энергетическое разрешение центрального сцинтилляционного счетчика ∆ Е_е/Е_е, то величина δ Е_е должна быть, по крайней мере, в 2 раза меньше, чем ∆ Е_е/Е_е, чтобы энергетическое разрешение ухудшилось за счет телесного угла 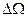не более, чем на 10%.

Комптоновский гамма-спектрометр с одним боковым кристаллом имеет эффективность около десятой доли процента. Эффективность его можно увеличить, если использовать несколько боковых кристаллов. Функция отклика комптоновского спектрометра показана на рис. 10.4, в пунктиром.

Существенно большей эффективностью и лучшим энергетическим разрешением обладают комптоновские спектрометры со сложением импульсов. Блок-схема такого спектрометра и расположение кристаллов показаны на рис. 4, б. В этом случае на анализатор импульсов направляется сумма импульсов с центрального и одного из боковых кристаллов при условии их совпадения во времени. Амплитуда импульса в центральном сцинтилляционном счетчике пропорциональна (Е – Е'), где Е и Е' – энергия падающего на кристалл и рассеянного в нем γ -кванта. Если рассеянный γ -квант поглотится в боковом кристалле, то импульс с бокового сцинтилляционного счетчика пропорционален Е'. Тогда амплитуда суммарного импульса пропорциональна энергии γ -кванта Е, если коэффициенты пропорциональности, которые связывают амплитуду импульса и энергию, поглощенную в кри­сталле во всех сцинтилляционных счетчиках, одинаковы. Так что независимо от угла рассеяния γ -кванта в центральном кристалле на анализ будут поступать импульсы с амплитудой, пропорциональной Е. Это позволяет располагать боковые кристаллы близко к центральному и за счет увеличения 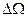достичь больших значений эффективности. Конечно, не каждый рассеянный в центральном кристалле γ -квант будет поглощен в боковом кристалле. Поэтому в амплитудном распределении G (Е, V)имеется кроме пика полного поглощения непрерывный континуум, площадь под которым тем меньше, чем больше размеры боковых кристал­лов. На рис. 4, в (сплошная линия) показано амплитудное распределение импульсов для γ -квантов изотопа ⁶⁵Zn, измеренное на спектрометре со сложением импульсов.

В комптоновском спектрометре со сложением импульсов удается получить энергетическое разрешение лучше, чем энергетическое разрешение отдельного сцин­тилляционного счетчика при энергии Е.

Сцинтилляционные парные гамма-спектрометры. Блок-схема и расположение кристаллов парного спектрометра показаны на рис. 10.5. Коллимированный пучок γ -квантов попадает в центральный кристалл, где в результате эффекта образования пар возникают электрон, позитрон и два фотона с энергией по 0, 511 Мэви углом между направлениями их движения 180°.

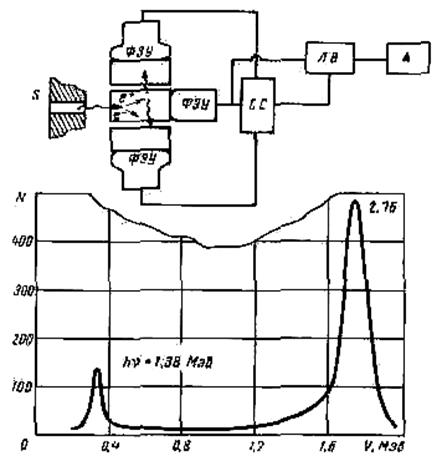
Рис. 10.5. Блок -схема парного сцинтилляционного спектрометра и его функция отклика для γ -квантов источника ²⁴Na

С помощью схемы тройных совпадений и линейных ворот с центрального сцинтилляционного счетчика отбираются такие импульсы, которые сопровождаются импульсами с двух боковых счетчиков.

Эффективность парного спектрометра будет определяться вероятностью образования пар в центральном кристалле, вероятностью прохождения аннигиляционного излучения через центральный кристалл без взаимодействия и вероятностью регистрации аннигиляционных квантов в боковых кристаллах:

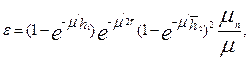
где h ₁ – высота центрального кристалла; – средний путь аннигиляционных квантов в центральном кристалле; 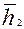– средний путь аннигиляционных квантов в боковых кристаллах; μ ' – полный линейный коэффициент ослабления аннигиляционного излучения в кристалле; μ _п и μ – линейный коэффициент образования пар и полный линейный коэффициент ослабления γ -квантов данной энергии.

Наилучшие условия работы парного спектрометра достигаются в тех случаях, когда исследуемое излучение хорошо коллимировано и не попадает на боковые кристаллы. При этом фон, обусловленный случайными совпадениями, оказывается невелик. Размеры центрального и боковых кристаллов выбирают, прини­мая во внимание следующие соображения. Чтобы получить боль­шую эффективность, центральный кристалл выгодно делать достаточно длинным. С одной стороны, это увеличивает эффективность спектрометра, с другой – уменьшает вероятность ухода электронов и позитронов из кристалла. Напомним, что электроны и позитроны, возникающие при эффекте образования пар, имеют направления, близкие к направлению пучка γ -квантов.

Диаметр центрального кристалла для получения наибольшей эффективности необходимо выбирать как можно меньше, поскольку вероятность ухода аннигиляционных квантов из центрального кристалла тем больше, чем меньше его диаметр. Но для спектрометра более важной характеристикой является его светосила, поэтому диаметр кристалла имеет смысл выбирать из условия получения ее максимальной величины. Светосила парного спектрометра пропорциональна диаметру коллиматора, т.е. сечению пучка γ -квантов, попадающих на центральный кристалл, и эффективности спектрометра. Оптимальный диаметр центрального кристалла около 30 мм.Однако обычно диаметр центрального кристалла выбирают несколько большего размера (до 40…50 мм)для лучших условий собирания света. Размеры боковых кристаллов парного спектрометра, с одной стороны, выгодно выбирать как можно большими, чтобы увеличить эффективность спектрометра, но, с другой стороны, чем больше размеры боковых кристаллов, тем больше регистрируется в них γ -квантов фона, естественной радиоактивности и космического излучения. Величина μ ' для аннигиляционного излучения в кристалле Nal(Tl) равна 0, 4 см^-1, поэтому высоту бокового кристалла нет смысла делать больше 4…5 см.Диаметр бокового кристалла обычно выбирают равным или несколько большим высоты центрального кристалла.

Эффективность парного спектрометра с центральным кристаллом диаметром 50 и высотой 100 мм и боковыми кристаллами диаметром 100 и высотой 50 ммдостигает нескольких процентов при энергии γ -квантов 10 Мэв.В зависимости от энергии γ -квантов эффективность спектрометра ведет себя практически так же, как и сечение образования пар.

Энергетическое разрешение парного спектрометра определяется качеством сцинтилляционного (центрального) счетчика. С помощью парного спектрометра можно разделять достаточно близкие по энергиям γ -кванты, если их энергии немного больше 2 m ₀с². В парном сцинтилляционном спектрометре в каналах боковых сцинтилляционных счетчиков обычно ставят одноканальные дифференциальные анализаторы для выбора импульсов, амплитуды которых соответствуют γ -квантам с энергией 0, 2…0, 6 Мэв.Это позволяет уменьшить фон случайных совпадений, фон, обусло­вленный многократным рассеянием γ -квантов в трех кристаллах, и наконец, снизить чувствительность парного спектрометра к нейтронам. На рис. 5 показано амплитудное распределение импульсов, измеренное с помощью парного спектрометра (фон случайных совпадений вычтен) для источника γ -квантов ²⁴Na (γ -кванты с энергиями 1, 38 и 2, 76 Мэв). Видно, что имеется непрерывное распределение импульсов, площадь которого составляет от полной около 10%. Это непрерывное распределение обусло­влено в основном тем, что пробеги электронов и позитронов не всегда укладываются в центральном кристалле. Утечки электронов и позитронов происходят главным образом через ближний к фотоумножителю торец кристалла.

Сцинтилляционные гамма-спектрометры с защитой антисовпадениями. Такие гамма-спектрометры являются наиболее современными и эффективными сцинтилляционными спектрометрами. Блок-схема такого спектрометра и расположение кристаллов показаны на рис. 10.6.

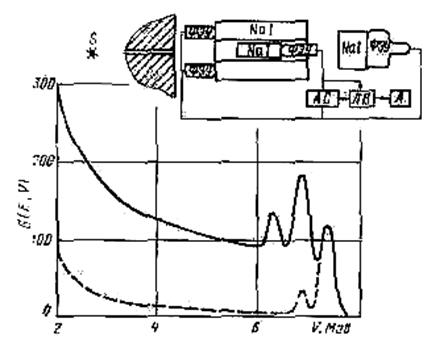
Рис. 10.6. Блок-схема сцинтилляционного гамма-спектрометра с защитой антисовпадениями. Спектр амплитуд импульсов γ -квантов с энергией 7, 38 Мэв без антисовпадений и с антисовпадениями (пунктир). АС–схема антисовпадений.

Коллимированный пучок γ -квантов попадает в центральный кристалл, импульсы с которого направляются на амплитудный анализатор при условии отсутствия импульсов с боковых кристаллов. Если бы боковые кристаллы регистрировали все рассеянные γ -кванты, выходящие из центрального кристалла, то аппаратурная форма линии такого спектрометра представляла бы собой пик полного поглощения. Как видно из рисунка, добиться 100%-ной вероятности регистрации рассеянных γ -квантов практически невозможно. Но боковые кристаллы значительно снижают непрерывное комптоновское распределение. На рис. 10.6 показаны аппаратурные формы линий спектрометра с включенным управлением антисовпадениями и без него. Эффективность спектрометра определяется эффективным фотовкладом, а энергетическое разрешение – качеством центрального сцинтилляционного счетчика. Один из таких спектрометров с очень хорошими параметрами описан ниже. Центральный кристалл спектрометра диаметром 60 и длиной 150 ммрасполагается в цилиндрическом отверстии большого кристалла диаметром 200 и длиной 300 мм.На небольшом расстоянии от центрального кристалла расположен третий кристалл диаметром 125 и толщиной 100 мм. Третий кристалл также включен на антисовпадения с центральным кристаллом. Этот кристалл необходим для регистрации γ -квантов, рассеянных на малые углы в центральном кристалле, и для регистрации тормозного излучения, рождаемого электронами и позитронами в центральном кристалле. Для описанного спектрометра энергетическое разрешение составляло 8, 3% при энергии γ -квантов 0, 66 Мэв. Эффективность спектро­метра изменяется от 100% при энергии γ -квантов в несколько сот килоэлектронвольт до 4% при энергии γ -квантов 10 Мэв. В спектрометрах с защитой антисовпадениями размеры боковых кристаллов не могут быть очень большими, поскольку загрузка фоновыми импульсами растет пропорционально объему кристаллов.

Полупроводниковая гамма-спектрометрия

В настоящее время наиболее перспективными полупроводниковыми спектрометрами для γ -квантов являются Ge(Li)-спектрометры, чувствительные объемы которых уже достигают нескольких сотен кубических сантиметров. Энергетическое разрешение в лучших спектрометрах составляет примерно 2…5 кэВв области энергий до 3 Мэв. Эффективность полупроводниковых спектрометров определяется чувствительным объемом детектора.

Основной недостаток полупроводниковых спектрометров – это сложная форма амплитудного распределения при регистрации моноэнергетического излучения. В связи с этим для улучшения формы линии используют Ge(Li)-спектрометр, работающий в совпадении или антисовпадении с кристаллами NaJ(Tl) больших объемов. Коаксиальный Ge(Li)-спектрометр объемом 30 см³(площадь 7, 5 см²)помещается внутрь цилиндрических кристаллов NaJ(Tl), как показано на рис. 10.13.

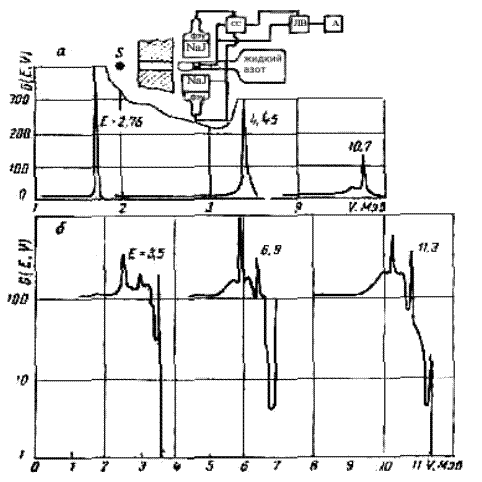
Рис. 10.13. Схема парного Ge(Li) – NaJ(Тl)-спектрометра: его функция отклика (а); функция отклика Ge(Li)-спектрометра объемом около 30 см³ (б).

Детектор работает при температуре 77° К, рабочее напряжение 900 в, емкость 42 п ф.Энер­гетическое разрешение спектрометра по пику полного поглощения (или парному пику) составляет около 0, 5% при энергии γ -квантов 1 Мэв(ширина пика примерно 5 кэв)и около 0, 2% при энергии γ -квантов 7 Мэв.На рис. 10.13, б показаны амплитудные распределения импульсов, полученные с Ge(Li)-спектрометром. Видно, что форма довольна сложная. Однако при использовании кристалла Nal(Tl) в режиме антисовпадений с Ge(Li) функция отклика значительно улучшается, как и в случае спектрометров с кристаллами NaJ(Tl). Эффективность по пику полного поглощения для этого случая показана на рис. 10.14.

При энергиях γ -квантов выше 2 Мэвоказывается выгодным режим работы парного спектрометра (совпадения импульса с Ge(Li)-спектрометра с двумя импульсами с кристаллов NaJ(Tl), обусловленных аннигиляционным излучением). В этом случае функция отклика (см. рис. 10.13) близка к идеальной. Эффективность парного Ge(Li)-спектрометра показана на рис. 10.14. Расчет эффективности спектрометра по пику полного поглощения, или эффективности парного спектрометра, аналогичен расчетам для сцинтилляционных спектрометров. В связи со сравнительно сложным видом функции отклика в некоторых случаях необходимо преобразовать амплитудные распределения в энергетические спектры. Для полупроводниковых детекторов эта задача усложняется в основном из-за необходимости составления матриц высокого порядка. Однако при изучении дискретных спектров в связи с хорошим энергетическим разреше­нием максимумы в распределениях достаточно хорошо выделены, и обычно достаточно знать эффективность спектрометра по пику полного поглощения (или парному пику).

В заключение сравним характеристики различных спектрометров, показанных на рис. 10.14.

Наибольшей эффективностью обладают сцинтилляционные спектрометры. К ним близки по эффективности полупроводниковые спектрометры. В этих приборах нет необходимости в значительном удалении источников от детекторов. С учетом необходимой коллимации излучения в спектрометрах совпадений и антисовпадений можно определить их светосилу. Для коллимации пучка γ -квантов в этих случаях обычно достаточны коллиматоры с углом 1, 0…2, 5°. Если использовать такие коллиматоры, то светосила L= (0, 7…5)·10^-4ε. Таким образом, светосила сцинтилляционных и полупроводниковых спектрометров на несколько порядков выше светосилы магнитных и кристалл-дифракционных спектрометров.

В области низких энергий γ -квантов с точки зрения энергетического разрешения наилучшими являются кристалл-дифракционные спектрометры. Причем чем ниже энергия γ -квантов, тем очевиднее их преимущества. В области энергий выше нескольких сот киловольт в широком диапазоне энергии преимущества на стороне полупроводниковых спектрометров.

Применение магнитных гамма-спектрометров с появлением такого перспективного конкурента, как полупроводниковые спектрометры, в настоящее время весьма ограниченно. Впрочем, магнитные гамма-спектрометры, значительно уступая полупроводниковым в светосиле, имеют и преимущества: возможность абсолютных измерений энергии γ -квантов и лучшая функция отклика.

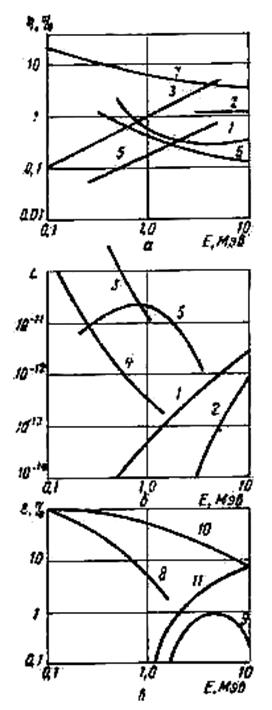
Рис. 10.14. разрешение, светосила н эффективность различных гамма-спектрометров: 1-магнитный комптоновский; 2-магнитный парный: 3-кристалл дифракционный типа Дю Монда; 4-кристалл дифракционный типа Кошуа; 5-кристалл-дифракционный с двумя плоскими кристаллами; 6-Ge(Li)-полупроводниковый спектрометр; 7-сцинтилляционный γ -спектрометр с кристаллом NaJ(Tl); 8-полупроводниковый Ge(Li)-спектрометр объемом 30 см³ по пику полного поглощения; 9-парный Ge(Li)- NaJ(Tl))-спектрометр; 10-спектрометр NaJ(Tl) с защитой антисовпадениями; 11-парный NaJ(Tl)-спектрометр.