Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Определение коэффициентов калибровочного графика графическим методом.

При количественных аналитических определениях приходится пользоваться линейными градуировочными графиками. Для их построения обычно анализируют серию образцов (эталонов). Результаты анализов могут быть представлены системой уравнений:

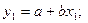
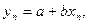…; (1)

где х₁, …, х_n – известная концентрация определяемого вещества в эталоне;

у₁, …, у_n – результаты прямых измерений; а и b – коэффициенты градуировочного графика, которые являются неизвестными величинами; n – число проанализированных проб.

Коэффициенты а и b могут быть вычислены из опытных данных со значением х₁, у₁; х₂, у₂ … строят график и записывают систему из n уравнений:

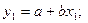
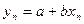. (2)

При вычислении коэффициентов а и b из этих уравнений может быть использована каждая пара, например:

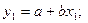
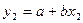. (3)

Так как значения коэффициентов а и b зависят от выбора пар уравнений, то рекомендуется брать не соседние уравнения, а стоящие на определенном расстоянии друг от друга. При этом неточности значений х и у меньше будут сказываться на значениях а и b.

При вычислении коэффициента b в паре уравнений отнимают второе уравнение от первого:

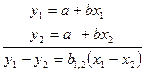, (4)

отсюда

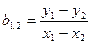. (5)

Индексы 1 и 2, стоящие при b, указывают, какие пары уравнений взяты для вычисления параметров b. Подставляя вычисленные значения b_{1, 2} вместо b в первое и второе из уравнений и складывая их, находят значения а_{1, 2} по формуле:

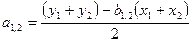. (6)

Для получения более достоверных значений коэффициентов берут еще одну пару уравнений:

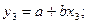
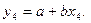(7)

Коэффициент b вычисляется так же, как в первом случае:

. (8)

При этом коэффициенты b_{1, 2} и b_{3, 4} неравны, т.е. b_{1, 2} ¹ b_{3, 4}. Среднее арифметическое коэффициента b рассчитывают по формуле:

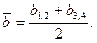(9)

Среднее арифметическое а для четырех взятых уравнений вычисляют по формуле:

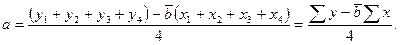(10)

Число пар уравнений для вычисления коэффициентов можно было бы еще увеличивать. Так, при использовании этого методов для определения коэффициентов а и b с достаточно высокой точностью можно ограничиться пятью уравнениями и тремя парами комбинаций:

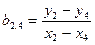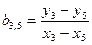; ; . (11)

Как видно, при принятых трех комбинациях пар использовано пять уравнений. В этом случае среднее значение коэффициента вычисляют по формуле:

(12)

Среднее значение коэффициента - по формуле:

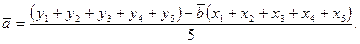(13)

Если сумму значений коэффициентов взятых пар уравнений обозначить 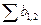, то среднее значение коэффициента находят по формуле:

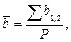(14)

где р – число пар уравнений.

Для вычисления :

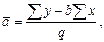(15)

где q – число уравнений, взятых из системы исходных.

Используя рассмотренные графические методы определения коэффициентов в линейном уравнении у=а+bх и заменив в нем значения коэффициентов а и b на вычисленные, т.е. приняв, что а=h (вычисленному) и b=e (вычисленному), получают общий вид уравнения калибровочного графика:

(16)

где y – рассчитанное количество вещества, определяемого по формуле.

Определив для калибровочного графика h и e, найдите неизвестную концентрацию раствора:

С_х=(n_x- h)/ e (17)