Критерии подобия. Как показано выше, законы подобия могут быть выведены из урав-нений, которые описывают реальные физические процессы

Как показано выше, законы подобия могут быть выведены из урав-нений, которые описывают реальные физические процессы. Но, наряду с законами подобия (коэффициентами подобия), существуют также безразмер-ные величины, которые также характеризуют физические процессы. Эти безразмерные величины называются критериями подобия.

Два физических процесса подобны, если все критерии подобия, описы-вающие эти процессы, попарно равны друг другу.

Если в уравнениях (5.4) и (5.5) заменить коэффициенты подобия отно-шениями физических величин

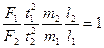, (5.6) то получим безразмерные величины, которые и являются критериями подобия:

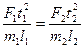. (5.7)

В динамике этот критерий подобия называется числом Ньютона Ne:

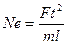или 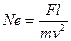. (5.8) Аналогичные коэффициенты подобия для сил тяжести имеют вид:

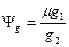или 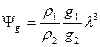, (5.9) а закон подобия переходит в выражение

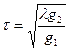. (5.10)

Это так называемый закон подобия Фруда, и критерий подобия Fr назы-вается числом Фруда:

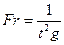или 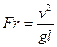. (5.11)

При течении реальных жидкостей возникают так называемые силы внутреннего трения

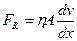, (5.12)

Коэффициент подобия силы трения вязкой жидкости равен

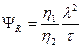. (5.13)

Если ввести кинематическую вязкость 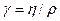, то получим закон подо-бия Рейнольдса

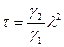. (5.14)

Соответствующий критерий подобия называется числом Рейнольдса Re.

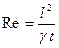или 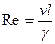. (5.15)

Это одна из важнейших величин в гидродинамике.

Для упругих сил, подчиняющихся закону Гука 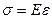, существует коэффициент подобия

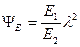, (5.16) где Е – модуль упругости; 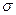– нормальное напряжение упругих сил;

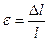– относительное удлинение (деформация).

Соответствующий закон подобия (закон Коши):

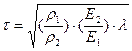, (5.17) а соответствующий критерий подобия называется числом Коши Са:

Са = 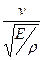. (5.18)

Из уравнения для коэффициента подобия (5.17) получается закон подобия Гука для упругих сил, причем коэффициенты Пуассона модель-ной системы и оригинала должны быть равны:

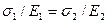. (5.19)

Соответствующий критерий подобия называется числом Гука Но:

Но = σ ₂/ Е. (5.20)

Законы подобия для термодинамических процессов. При решении задач теплопереноса необходимо учитывать теплопроводность, конвекцию, а также теплообмен между твердыми телами, жидкостями и газами.

Применение законов подобия позволяет обобщить термодинамические процессы в различных системах на основе модельных экспериментов.

Если две системы термически подобны, то температуры в соот-ветственных точках модели и оригинала связаны соотношением:

Т₁ = θ Т₂. (5.21)

Воспользовавшись дифференциальным уравнением теплопереноса

,

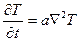получим закон подобия Фурье

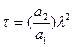, (5.22) где а₁; а₂ – коэффициенты температуропроводности для оригинала и модели соответственно.

Критерием подобия в данном случае является число Фурье Fo:

Fo = 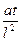. (5.23)

Всякая новая комбинация из критериев подобия также является крите-рием подобия. Так, например, величина 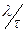из выражения (5.23) является ко-эффициентом подобия для скорости. В этом случае (5.23) называют законом подобия Пекле, а соответствующий критерий подобия – числом Пекле Ре:

Ре = 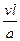. (5.24)

Примерами критериев подобия для электромагнитных полей служат критери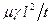и: и 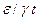, где μ – магнитная проницаемость среды; ε – диэлектрическая проницаемость среды; γ – удельная проводимость среды. Критерии подобия для движения заряженных частиц, движущихся в электрическом и магнитном полях, имеют вид:

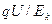и 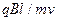. (5.25)