Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач
|
|
Пример 1. Два параллельных бесконечно длинных провода D и С, по которым текут в одном направлении электрические токи силой I=60A, расположены на расстоянии d=10 см друг от друга. Определить магнитную индукцию В поля, создаваемого проводниками с током в точке А (рис.1), отстоящей от оси одного проводника на расстоянии r1=5 cм, от другого - r2=12 cм.
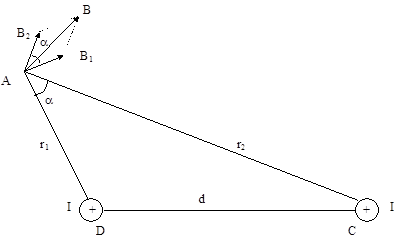
|
Рис.1
Решение: Для нахождения магнитной индукции В в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукций В1 и В2 полей, создаваемых каждым проводником с током в отдельности, и сложим их векторно:
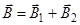 .
.
Модуль вектора 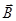 может быть найден по теореме косинусов:
может быть найден по теореме косинусов:
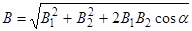 , (1)
, (1)
где a - угол между векторами  и
и 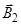 .
.
Магнитные индукции  и
и 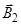 выражаются соответственно через силу тока I и расстояния r1 и r2 от проводов до точки А:
выражаются соответственно через силу тока I и расстояния r1 и r2 от проводов до точки А:
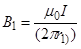 ;
;  .
.
Подставляя выражения В1 и В2 в формулу (1) и вынося  за знак корня, получаем
за знак корня, получаем
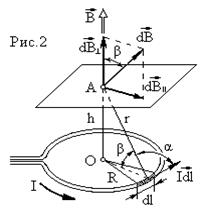
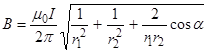 . (2)
. (2)
Вычислим cos a. Заметив, что a=Ð DCA (как углы с соответственно перпендикулярными сторонами), по теореме косинусов запишем
 ,
,
где d - расстояние между проводами. Отсюда
 ;
; 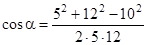 .
.
Подставим в формулу (2) числовые значения физических величин и произведем вычисления:
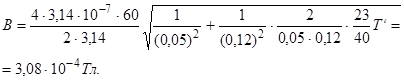
Пример 2. По тонкому проводящему кольцу радиусом R =10 см течет ток I =80 А. Найти магнитную индукцию 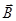 в точке А, равноудаленной от всех точек кольца на расстояние r =20 см.
в точке А, равноудаленной от всех точек кольца на расстояние r =20 см.
Решение: Для решения задачи воспользуемся законом Био-Савара-Лапласа:
 ,
,
где 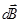 - магнитная индукция поля, создаваемого элементом тока
- магнитная индукция поля, создаваемого элементом тока 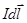 в точке, определяемой радиусом-вектором
в точке, определяемой радиусом-вектором 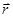 .
.
Выделим на кольце элемент 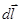 и от него в точку А проведем радиус-вектор
и от него в точку А проведем радиус-вектор 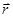 (рис.2). Вектор
(рис.2). Вектор  направим в соответствии с правилом буравчика.
направим в соответствии с правилом буравчика.
Согласно принципу суперпозиции магнитных полей, магнитная индукция  в точке А определяется интегрированием:
в точке А определяется интегрированием:
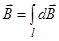 ,
,
где интегрирование ведется по всем элементам dl кольца.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Разложим вектор  на две составляющие:
на две составляющие: 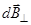 , перпендикулярную плоскости
, перпендикулярную плоскости
кольца, и 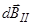 , параллельную плоскости кольца, т.е.
, параллельную плоскости кольца, т.е.
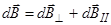
Тогда
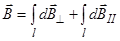
Заметив, что 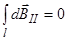 из соображений симметрии и что векторы
из соображений симметрии и что векторы  от различных элементов
от различных элементов 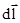 сонаправлены, заменим векторное суммирование (интегрирование) скалярным:
сонаправлены, заменим векторное суммирование (интегрирование) скалярным:
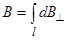 ,
,
где 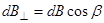 и
и 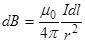 (поскольку
(поскольку 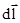 перпендикулярен
перпендикулярен  и, следовательно, sin a=1). Таким образом,
и, следовательно, sin a=1). Таким образом,
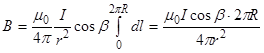 .
.
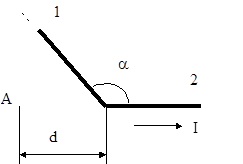
|
После сокращения на 2p и замены cos b на R/r (рис.2) получим
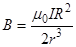 или
или 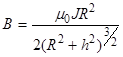 ,
,
где h – расстояние от плоскости кольца до точки А.
Проверим, дает ли правая часть равенства единицу магнитной индукции (Тл):
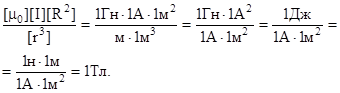
Здесь мы воспользовались определяющей формулой для магнитной индукции:
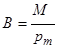 .
.
Тогда
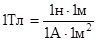 .
.
Выразим все величины в единицах СИ и произведем вычисления:
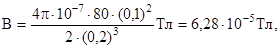 или В=62, 8 мкТл.
или В=62, 8 мкТл.
Вектор  направлен по оси кольца (пунктирная стрелка на рис) в соответствии с правилом буравчика.
направлен по оси кольца (пунктирная стрелка на рис) в соответствии с правилом буравчика.
Пример 3. Длинный провод с током I=50 A изогнут под углом a=2p/3. Определить магнитную индукцию В в точке А (рис.3). Расстояние d=5 см.
Решение: Изогнутый провод можно рассматривать как два длинных провода, концы которых соединены в точке О (рис.4). В соответствии с принципом суперпозиции магнитных полей магнитная индукция В в точке А будет равна векторной сумме магнитных индукций 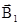 и
и  полей, создаваемых отрезками длинных проводов 1 и 2, т.е.
полей, создаваемых отрезками длинных проводов 1 и 2, т.е. 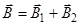 . Магнитная индукция В2 равна нулю. Это следует из закона Био-Савара-Лапласа, согласно которому в точках, лежащих на оси привода, dB = 0 ([
. Магнитная индукция В2 равна нулю. Это следует из закона Био-Савара-Лапласа, согласно которому в точках, лежащих на оси привода, dB = 0 ([ 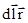 ] = 0).
] = 0).
Магнитную индукцию В1 найдем, воспользовавшись соотношением (3), найденным в примере 1:

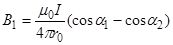
где r0 - кратчайшее расстояние от провода 1 до точки А (рис.4).
В нашем случае a1®0 (провод длинный), a2 = a = 2p/3 (сos a2 = =cos (2p/3) = -1/2). Расстояние r0 = d sin (p-a) = d sin (p/3) = d 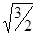 . Тогда магнитная индукция
. Тогда магнитная индукция
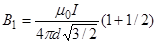 .
.
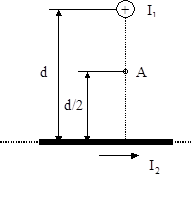
|
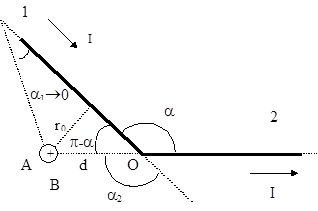
Рис.4.
Так как B = B1 (B2 = 0), то
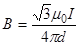
Вектор  сонаправлен с вектором
сонаправлен с вектором 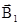 и определяется правилом правого винта. На рис.4 это направление отмечено крестиком в кружочке (перпендикулярно плоскости чертежа, от нас).
и определяется правилом правого винта. На рис.4 это направление отмечено крестиком в кружочке (перпендикулярно плоскости чертежа, от нас).
Проверка размерности аналогична выполненной в примере 2. Произведем вычисления:
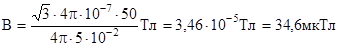 .
.
Пример 4. Два бесконечно длинных провода скрещены под прямым углом (рис.5). По проводам текут токи I1 = 80 A и I2 =60 A. Расстояние d между проводами равно 10 см. Определить магнитную индукцию  в точке А, одинаково удаленной от обоих проводов.
в точке А, одинаково удаленной от обоих проводов.
Решение. В соответствии с принципом суперпозиции магнитных полей магнитная индукция  поля, создаваемого токами I1 и I2, определяется выражением
поля, создаваемого токами I1 и I2, определяется выражением 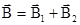 , где
, где 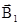 - магнитная индукция поля, созданного в точке А током I1;
- магнитная индукция поля, созданного в точке А током I1;  - магнитная индукция поля, созданного в точке А током I2. Заметим, что векторы
- магнитная индукция поля, созданного в точке А током I2. Заметим, что векторы 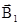 и
и  взаимно перпендикулярны (их направления находятся по правилу буравчика и изображены в двух проекциях на рис.6). Тогда модуль вектора
взаимно перпендикулярны (их направления находятся по правилу буравчика и изображены в двух проекциях на рис.6). Тогда модуль вектора  можно определить по теореме Пифагора:
можно определить по теореме Пифагора:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе

где В1 и В2 определяются по формулам расчета магнитной индукции для бесконечно длинного прямолинейного провода с током:
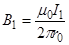 и
и 
В нашем случае r0 = d/2. Тогда
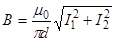
Проверка размерности аналогична выполненной в примере2. Произведем вычисления:
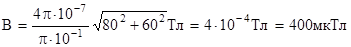
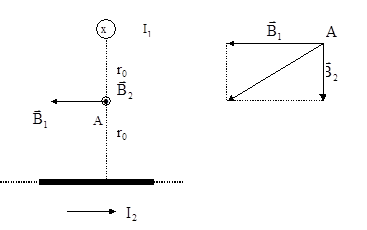
|
Пример 5. Бесконечно длинный провод изогнут так, как это изображено на рис. 7. Радиус R дуги окружности равен 10 см. Определить магнитную индукцию  поля, создаваемого в точке О током I = 80 A, текущим по этому проводу.
поля, создаваемого в точке О током I = 80 A, текущим по этому проводу.
Решение. Магнитную индукцию  в точке О найдем, используя принцип суперпозиции магнитных полей:
в точке О найдем, используя принцип суперпозиции магнитных полей: 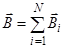 . В нашем случае провод можно разбить на три части (рис.8): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда
. В нашем случае провод можно разбить на три части (рис.8): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда
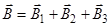
где 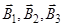 - магнитные индукции в точке О, создаваемые током, текущим соответственно на первом, втором и третьем участках провода.
- магнитные индукции в точке О, создаваемые током, текущим соответственно на первом, втором и третьем участках провода.
Так как точка О лежит на оси провода 1, то В 1 = 0 и тогда
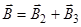
 |
Рис.7. Рис.8.
Учитывая, что векторы 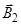 и
и 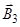 направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, то векторное суммирование можно заменить алгебраическим:
направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, то векторное суммирование можно заменить алгебраическим:
В = В2 + В3
Магнитную индукцию В2 найдем, воспользовавшись выражением для магнитной индукции в центре кругового тока:
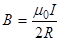
В нашем случае магнитное поле в точке О создается лишь половиной такого кругового тока, поэтому
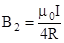
Магнитную индукцию  найдем по формуле:
найдем по формуле:
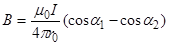
В нашем случае r0 = R, a1=p/a (cos a1 = 0), a2®p (cos a2 = -1). Тогда


Используя найденные выражения для В2 и В3, получим
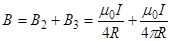
или
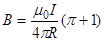
Проверка размерности аналогична выполненной в примере 2.
Произведем вычисления:
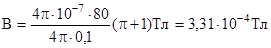 ,
,
или
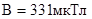
Пример 6. Протон, прошедший ускоряющую разность потенциалов U = 600 В, влетел в однородное магнитное поле с индукцией В = 0, 3 Тл и начал двигаться по окружности. Вычислить радиус R окружности.
Решение. Движение заряженной частицы в однородном магнитном поле будет происходить по окружности только в том случае, когда частица влетит в магнитное поле перпендикулярно линиям магнитной индукции  . Так как сила Лоренца
. Так как сила Лоренца 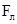 перпендикулярна вектору
перпендикулярна вектору 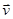 , то она сообщит частице (протону) нормальное ускорение аn.
, то она сообщит частице (протону) нормальное ускорение аn.
Согласно второму закону Ньютона,
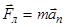 (1)
(1)
где m - масса протона.
На рис. 9 совмещена траектория протона с плоскостью чертежа и дано (произвольно) направление вектора 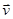 . Силу Лоренца направим перпендикулярно вектору
. Силу Лоренца направим перпендикулярно вектору 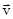 к центру окружности (векторы
к центру окружности (векторы 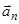 и
и 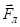 сонаправлены). Используя правило левой руки, определим направление линий индукции (направление вектора
сонаправлены). Используя правило левой руки, определим направление линий индукции (направление вектора 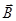 ).
).
|
|
|
|
|

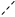



|


























| |||||
| |||||
 |
Рис.9.
Перепишем выражение (1) в скалярной форме (в проекции на радиус):
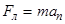 (2)
(2)
В скалярной форме FЛ = QvBsin a. В нашем случае 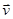 ^
^ 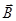 и sin a=1, тогда FЛ = QvB. Так как нормальное ускорение an = v2/R, то выражение (2) перепишем следующим образом:
и sin a=1, тогда FЛ = QvB. Так как нормальное ускорение an = v2/R, то выражение (2) перепишем следующим образом:
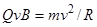
Отсюда находим радиус окружности:
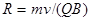
Заметив, что mv есть импульс протона (p), это выражение можно записать в виде
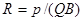 (3)
(3)
Импульс протона найдем, воспользовавшись связью между работой сил электрического поля и изменением кинетической энергии протона, т.е. А = DТ, или
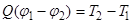
где j1 - j2 - ускоряющая разность потенциалов (или ускоряющее напряжение U); Т 1 и Т 2 - начальная и конечная кинетические энергии протона.
Пренебрегая начальной кинетической энергией протона (Т 1»0) и выразив кинетическую энергию Т 2 через импульс p, получим
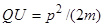
Найдем из этого выражения импульс  и подставим его формулу (3):
и подставим его формулу (3):
 ,
,
или
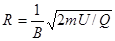 (4)
(4)
Убедимся в том, что правая часть равенства дает единицу длины (м):

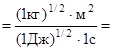
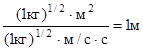 .
.
Подставим в формулу (4) числовые значения физических величин и произведем вычисления:
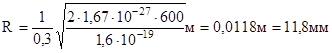
Пример 7. Электрон, влетев в однородное магнитное поле (В = 0, 2 Тл), стал двигаться по окружности радиуса R = 5 cм. Определить магнитный момент pm эквивалентного кругового тока.
Решение. Электрон начинает двигаться по окружности, если он влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции. На рис.10 линии магнитной индукции перпендикулярны плоскости чертежа и направлены “от нас” (обозначены крестиками).
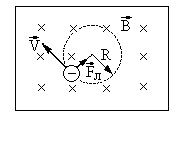
Рис.10.
Движение электрона по окружности эквивалентно круговому току, который в данном случае определяется выражением
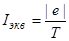
где е - заряд электрона; Т - период его обращения.
Период обращения можно выразить через скорость электрона v и путь, проходимый электроном за период
T = (2pR/v). Тогда
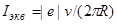 (1)
(1)
Зная I экв, найдем магнитный момент эквивалентного кругового тока. По определению, магнитный момент контура с током выражается соотношением
 (2)
(2)
где S - площадь, ограниченная окружностью, описываемой электроном (S = pR 2).
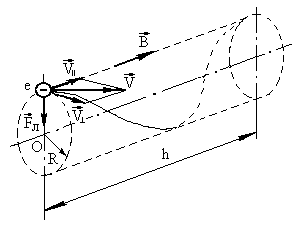 Подставив I экв из (1) в выражение (2), получим
Подставив I экв из (1) в выражение (2), получим
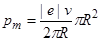
Сократим на p R и перепишем это выражение в виде:
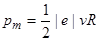 (3)
(3)
В полученном выражении известной является скорость электрона, которая связана с радиусом R окружности, по которой он движется, соотношением R = mv/(QB) (см. пример 6). Заменив Q на |е|, найдем интересующую нас скорость v = |e|BR/m и подставим ее в формулу (3):
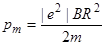
Убедимся в том, что правая часть равенства дает единицу измерения магнитного момента (А× м2):
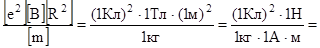
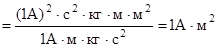
Произведем вычисления:
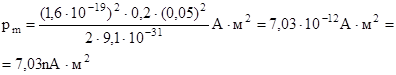
Пример 8. Электрон движется в однородном магнитном поле (В = 10 мТл) по винтовой линии, радиус R которой равен 1 см и шаг h = 6 см. Определить период T обращения электрона и его скорость v.
|
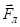 ^
^ 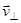 ) (в отсутствие параллельной составляющей, v || = 0, движение электрона происходило бы по окружности в плоскости, перпендикулярной линиям индукции). Таким образом, электрон будет участвовать одновременно в двух движениях: равномерном перемещении со скоростью v || и равномерном движении по окружности со скоростью v ^.
) (в отсутствие параллельной составляющей, v || = 0, движение электрона происходило бы по окружности в плоскости, перпендикулярной линиям индукции). Таким образом, электрон будет участвовать одновременно в двух движениях: равномерном перемещении со скоростью v || и равномерном движении по окружности со скоростью v ^.
Период обращения электрона связан с перпендикулярной составляющей скорости соотношением:
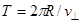 (1)
(1)
Найдем отношение R/v ^. Для этого воспользуемся тем, что сила Лоренца сообщает электрону нормальное ускорение an = v^2 /R. Согласно второму закону Ньютона можно написать
 ,
,
или
 (2)
(2)
где v^ = v sin a.
Сократив (2) на v ^, выразим соотношение R/v ^ (R/v^ = m/|e|B)и подставим его в формулу (1):
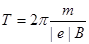
Убедимся в том, что правая часть равенства дает единицу времени (с):
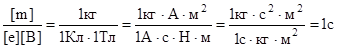
Произведем вычисления:

Модуль скорости v, как это видно из рис.11, можно выразить через v^ и v|| :
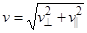
Из формулы (2) выразим перпендикулярную составляющую скорости:
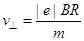

Параллельную составляющую скорости v || найдем из следующих соображений. За время, равное периоду обращения T, электрон пройдет в направлении магнитного поля расстояние, равное шагу винтовой линии, т.е. h = Tv ||, откуда
v|| = h/T
Подставив вместо Т правую часть выражения (2), получим
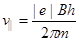
Таким образом, модуль скорости электрона
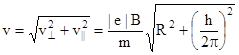
Убедимся в том, что правая часть равенства дает единицу скорости (м/с). Для этого заметим, что R и h имеют одинаковую единицу измерения - метр (м). Поэтому в квадратных скобках мы поставим только одну из величин (например, R):
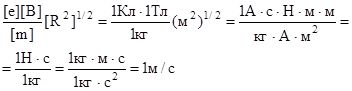
Произведем вычисления:
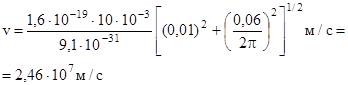
или 24, 6 Мм/с.
Пример 9. Рамка, содержащая N = 103 витков, равномерно вращается с частотой n = 10 c-1 относительно оси АВ, лежащей в плоскости рамки и перпендикулярной линиям однородного магнитного поля (В = 0, 04 Тл). Определить мгновенное значение ЭДС индукции для тех моментов времени, когда плоскость рамки составляет угол a= 60° с линиями поля. Площадь S рамки равна 100 см2.
Решение. Мгновенное значение ЭДС индукции ei определяется основным уравнением электромагнитной индукции Фарадея-Максвелла:
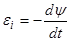 (1)
(1)
Потокосцепление Y = NФ, где N - число витков рамки, пронизываемых магнитным потоком Ф. Подставив выражение Y в формулу (1), получим
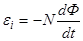 (2)
(2)
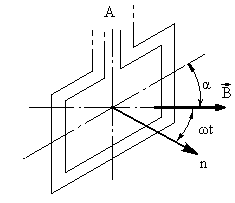
Рис.12
При вращении рамки магнитный поток Ф, пронизывающий рамку в момент времени t, изменяется по закону Ф = BS cos wt, где B - магнитная индукция; S - площадь рамки; w - угловая скорость рамки. Подставив в формулу (2) выражение магнитного потока Ф и продифференцировав по времени, найдем мгновенное значение ЭДС индукции:
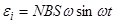
Заметив, что угловая скорость w cвязана с частотой вращения n рамки соотношением w = 2pn и что угол wt = p/2 - a (рис.11), получим (учтено, что sin (p/2-a) = cos a)
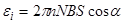
Убедимся в том, что правая часть этого равенства дает единицу ЭДС (В):
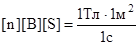
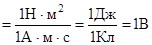
Произведем вычисления:
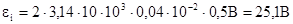
Пример 10. Квадратная проволочная рамка со стороной а = 5 см и сопротивлением R = 10 мОм находится в однородном магнитном поле (В = 40 мТл). Нормаль к плоскости рамки составляет угол a = 30° с линиями магнитной индукции. Определить заряд Q, который пройдет по рамке, если магнитное поле выключить.
Решение. При выключении магнитного поля произойдет изменение магнитного потока. Вследствие этого в рамке возникнет ЭДС индукции, определяемая основным законом электромагнитной индукции
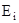

Возникшая ЭДС индукции вызовет в рамке индукционный ток, мгновенное значение которого можно определить воспользовавшись законом Ома для полной цепи Ii = ei/R, где R - сопротивление рамки. Тогда
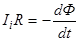
Так как мгновенное значение силы индукционного тока 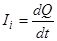 , то выражение можно переписать в виде
, то выражение можно переписать в виде
 , откуда
, откуда 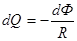 (1)
(1)
Проинтегрировав выражение (1), найдем
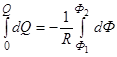 , или
, или 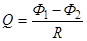
Заметим, что при выключенном поле (конечное состояние) Ф 2 = 0, последнее равенство перепишется в виде
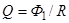 (2)
(2)
Найдем магнитный поток Ф 1. По определению магнитного потока имеем
Ф 1 = ВS cos a
где S - площадь рамки.
В нашем случае (рамка квадратная) S = a 2. Тогда
Ф1 = Ва 2сos a(3)
Подставив (3) в (2), получим

Убедимся в том, что правая часть этого равенства дает единицу заряда (Кл):
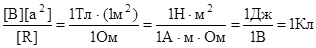
Произведем вычисления:

Пример 11. Плоский квадратный контур со стороной а = 10 см, по которому течет ток I = 100 A, свободно установился в однородном магнитном поле (В = 1 Тл). Определить работу А, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) j=90°; 2)j=3°. При повороте контура сила тока в нем поддерживается неизменной.
Решение. Как известно, на контур с током в магнитном поле действует момент силы.
М = pmB sin j (1)
где pm = IS = Ia 2 - магнитный момент контура; B - магнитная индукция; j - угол между векторами 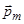 (направлен по нормали к контуру) и
(направлен по нормали к контуру) и 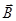 .
.
По условию задачи в начальном положении контур свободно установился в магнитное поле. При этом момент силы равен нулю (М = 0), а значит, j = 0, т.е. векторы 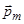 и
и  сонаправлены. Если внешние силы выведут контур из положения равновесия, то возникший момент сил будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота j), то для подсчета работы применим формулу работы в дифференциальной форме dA = Мd j.Учитывая формулу (1), получаем
сонаправлены. Если внешние силы выведут контур из положения равновесия, то возникший момент сил будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота j), то для подсчета работы применим формулу работы в дифференциальной форме dA = Мd j.Учитывая формулу (1), получаем
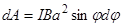
Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол:
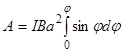 (2)
(2)
Работа при повороте на угол j1 = 90°
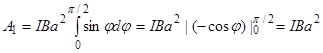 (3)
(3)
Выразим числовые значения величин в единицах СИ (I = 100 A, B = 1Tl, a = 10 см = 0, 1 м) и подставим в (3):
A1 = 100× 1× (0, 1)2 Дж = 1 Дж
Работа при повороте на угол j2 = 3°. В этом случае, учитывая, что угол j2 мал, заменим в выражении (2) sin j»j:
 (4)
(4)
Выразим угол j2 в радианах. После подстановки числовых значений величин в (4) найдем
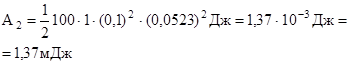
Задачу можно решить и другими способами:
1. Работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, пронизывающего контур:
А = -IDФ = I(Ф1 - Ф2)
где Ф 1 - магнитный поток, пронизывающий контур до перемещения; Ф 2 - то же, после перемещения.
Если j = 90°, то Ф1 = BS, Ф2 = 0. Следовательно,
А = IBS = IBa 2
что совпадает с (3).
2. Воспользуемся выражением для механической потенциальной энергии контура с током в магнитном поле
П (j) = -pmBcosj
Тогда работа внешних сил
А = DP = P2 - P 1 или А = pmB (cosj1 - cosj2)
Так как pm = Ia2, cos j1 = I и cos j2 = 0, то
А = Iba2
что также совпадает с (3).
КОНТРОЛЬНЫЕ ВОПРОСЫ
|
|