Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Порядок расчетов

1. По имеющимся материалам (получают у преподавателя) статистического учета одного из метамерных признаков заданного числа (определяет преподаватель) растений в популяции осуществляют расчет основных статистик и определяют точность опытных данных. В случае достаточного уровня точности (не более 5%) приступают к собственно дисперсионному анализу по предлагаемому ниже алгоритму.

2. Исходные данные группируют в виде комбинационной таблицы таким образом, чтобы градации регулируемого (в нашем случае учитываемого) фактора (в нашем случае – это различия в генетической природе особей) располагались по горизонтали в верхней части таблицы. Обозначим действующий фактор через «А». Тогда в верхней горизонтальной строке таблицы окажутся порядковые номера учетных растений, соответствующие градациям действующего фактора (каждое растение – самостоятельная градация). Градации фактора «А» образуют столбцы, в которых располагаются варьирующие значения результативного признака (проявление в границах случайной изменчивости формирования признаков в пределах отдельной градации). Их называют вариантами или датами и обозначают «x_i». Они группируются по соответствующим градациям фактора А.

Таблица

3. Принимаем основные алгоритмы вычислений в дисперсионном анализе.

3.1. Общая сумма квадратов отклонений, которая в рабочих алгоритмах чаще используется в виде правой части равенства.

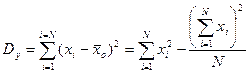
3.2. Межгрупповая (факториальная) сумма квадратов отклонений.

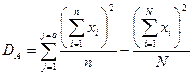
3.3. Внутригрупповую, или остаточную, сумму квадратов отклонений определяют по разности между общей и межгрупповой суммами квадратов отклонений.

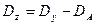
3.4. Числа степеней свободы определяем по следующим формулам:

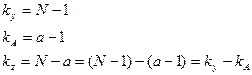
3.5. Определяют средние квадраты отклонений или дисперсии: их находят через отношение соответствующих сумм квадратов отклонений к соответствующим степеням свободы.

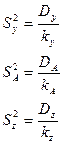
3.6. Определяют эффективность действия фактора А (в нашем случае эффективность действия фактора различий между особями) на результирующий признак (в нашем случае на конкретное проявление признака каждой особью). Для этого используют дисперсионное отношение или критерий Фишера F.

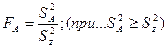
Так как дисперсионное отношение – величина случайная, его сравнивают с табличным (стандартным) значением.

3.7. В предложенном алгоритме расчета дисперсионного отношения можно легко увидеть некоторое общее содержание конкретных формул (в расчете общего квадрата отклонений и в расчете факториального квадрата отклонений). Эту общую часть часто выражают знаком Н.

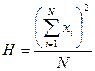
4. Если доказана достоверность влияния действующего фактора, то с помощью дисперсионного анализа можно определить и силу его влияния на результирующий признак. Силу влияния фактора определяют как долю факториальной или межгрупповой изменчивости в общем варьировании признака. Существует ряд способов расчета этого показателя. Наиболее распространенными являются способ Плохинского (1966, 1970) и способ Снедекора (1961).

4.1. При реализации способа Плохинского исходят из того, что справедливо равенство D_y=D_x+D_z, которое осуществляется в любом дисперсионном комплексе. В этом способе расчета оперируют суммами квадратов отклонений. Делением всех членов этого равенства на D_y получают:

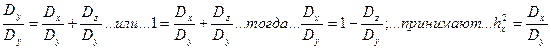
Показатель h² принимают как силу влияния действующего фактора, и в ряде случаев его рассматривают как показатель степени наследственной обусловленности различий между особями или как коэффициент наследуемости. (****УТОЧНИТЬ***).

Критерием достоверности этого показателя служит его отношение к своей ошибке, которая вычисляется по следующей приближенной формуле:

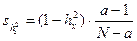, где

a – число градаций фактора А;

N – общее число вариант.

Нулевая гипотеза отвергается если

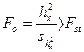
Стандартное значение критерия Фишера берется по таблице, При этом учитывают заданный уровень значимости и число степеней свободы: k₁=a-1 (находится в верхней горизонтальной строке таблицы), k₂=N-a (находится в первом вертикальном столбце таблицы).

ЗАДАНИЕ к пункту 4.1.

Выполните расчет значений коэффициента наследуемости в широком смысле по методу Плохинского, используя исходный материал, полученный у преподавателя.

4.2. В способе Снедекора в качестве показателя силы влияния используют отношение межгрупповой дисперсии к общей дисперсии для всего комплекса, которая определяется как сумма дисперсий межгрупповой и остаточной:

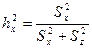
При этом межгрупповая дисперсия определяется с учетом влияния на групповые характеристики комплекса случайных нерегулируемых факторов (различия между особями обусловлены не только влиянием собственно различиями в их происхождении, но и различиями в условиях произрастания каждого из них). Расчет факториальной дисперсии в этом случае ведут по формуле

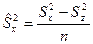, где

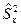- факториальная дисперсия, без дисперсии, вызванной влиянием среды;

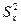- межгрупповой средний квадрат отклонений или «неисправленная» межгрупповая

дисперсия;

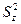- остаточная дисперсия;

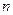- численность вариант в отдельных группах (градациях действующего фактора)

дисперсионного комплекса

Если числа вариант в градациях комплекса неодинаковы (неравномерный дисперсионный комплекс), то величина n определяется по формуле:

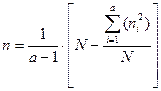, где

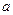- число градаций фактора А (в расчетах по нашему примеру – это число особей в выборке);

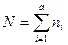- общее число наблюдений в дисперсионном комплексе;

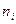- число наблюдений в пределах каждой из градаций фактора А.

Тогда показатель силы влияния фактора приобретает следующее выражение:

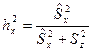
Достоверность показателя силы влияния фактора, определяемого по методу Снедекора, устанавливается обычным в дисперсионном анализе способом, т.е. посредством дисперсионного отношения (критерия Фишера)

,

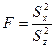величина которого сравнивается с критическим табличным значением для принятого уровня значимости и чисел степеней свободы k_x = а-1и k_z=N-a.

ЗАДАНИЕ к пункту 4.2.

Выполните расчет значений коэффициента наследуемости в широком смысле по методу Снедекора, используя исходный материал, полученный у преподавателя.

4. Вычисление значений коэффициента наследуемости в узком смысле.